Analysis of group differences in processing speed: where are the models of processing?

Abstract

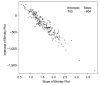
Recently, Myerson, Adams, Hale, and Jenkins (2003) replied to arguments advanced by Ratcliff, Spieler, and McKoon (2000) about interpretations of Brinley functions. Myerson et al. (2003) focused on methodological and terminological issues, arguing that (1) Brinley functions are not quantile-quantile (QQ) plots of distributions of mean reaction times (RTs) across conditions; that the fact that the slope of a Brinley function is the ratio of the standard deviations of the two distributions of means has no implications for the use of slope as a measure of processing speed; that the ratio of slopes of RT functions for older and young subjects plotted against independent variables equals the Brinley function slope; and that speed-accuracy criterion effects do not account for slowing with age. We reply by showing that Brinley functions are plots of quantiles against quantiles; that the slope is best estimated by the ratio of standard deviations because there is variability in the distributions of mean RTs for both older and young subjects; that the interpretation of equality of the slopes Brinley functions and plots of RTs against independent variables in terms of processing speed is model dependent; and that speed-accuracy effects in some, but not all, experiments are solely responsible for Brinley slopes greater than 1. We conclude by reiterating the point that was not addressed in Myerson et al. (2003), that the goal of research should be model-based accounts of processing that deal with correct and error RT distributions and accuracy.

Figure 1

A plot of intercept and slopes from Brinley functions when there is random variation across 200 simulated experiments in the overall means and SDs across conditions. For each simulated experiment, for older subjects, a mean RT was selected from a normal distribution with mean 700 msec and SD 70 msec, and an SD was selected from a normal distribution with mean 150 msec and SD 30 msec. For young subjects, a mean RT was selected from a normal distribution with mean 600 msec and SD 50 msec, and an SD was selected from a normal distribution with mean 100 msec and SD 20 msec. The Brinley slope and intercept were calculated for each of the 200 simulated experiments, and these provide the basis of the plot.

Figure 2

A Brinley function for the data from three experiments in Ratcliff etal. (2001, Experiment1 filled circles, Experiment 2 open triangles and filled squares) and Thapar et al. (2003, open circles and filled triangles). The top plot does not have error bars; the bottom plot is for the same data with ± 2 SE error bars.

Figure 3

An illustration of predictions from a serial processing model and a diffusion model applied to mean RT. The RT values are derived from a diffusion model with parameters: Condition A, a = 0.08, T_er = 0.3, η = 0.08, S_z = 0.02 drift rates 0.2 and 0.4, and S_t = 0.1; and Condition B, a = 0.12, T_er = 0.35, η = 0.08, S_z = 0.02, drift rates 0.2 and 0.4, and S_t = 0.1. a = boundary separation, T_er = nondecision component of RT, η = SD in drift across trials, S_z = range in starting point across trials, and S_t = and range in the distribution of T_er.