Creep function of a single living cell
- PMID: 15596508
- PMCID: PMC1305272
- DOI: 10.1529/biophysj.104.050278
Creep function of a single living cell
Abstract
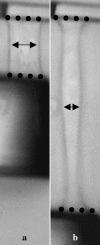
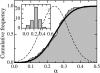
We used a novel uniaxial stretching rheometer to measure the creep function J(t) of an isolated living cell. We show, for the first time at the scale of the whole cell, that J(t) behaves as a power-law J(t) = At(alpha). For N = 43 mice myoblasts (C2-7), we find alpha = 0.24 +/- 0.01 and A = (2.4 +/- 0.3) 10(-3) Pa(-1) s(-alpha). Using Laplace Transforms, we compare A and alpha to the parameters G(0) and beta of the complex modulus G*(omega) = G(0)omega(beta) measured by other authors using magnetic twisting cytometry and atomic force microscopy. Excellent agreement between A and G(0) on the one hand, and between alpha and beta on the other hand, indicated that the power-law is an intrinsic feature of cell mechanics and not the signature of a particular technique. Moreover, the agreement between measurements at very different size scales, going from a few tens of nanometers to the scale of the whole cell, suggests that self-similarity could be a central feature of cell mechanical structure. Finally, we show that the power-law behavior could explain previous results first interpreted as instantaneous elasticity. Thus, we think that the living cell must definitely be thought of as a material with a large and continuous distribution of relaxation time constants which cannot be described by models with a finite number of springs and dash-pots.
Figures









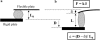

Similar articles
-
Probing mechanical properties of living cells by atomic force microscopy with blunted pyramidal cantilever tips.Phys Rev E Stat Nonlin Soft Matter Phys. 2005 Aug;72(2 Pt 1):021914. doi: 10.1103/PhysRevE.72.021914. Epub 2005 Aug 29. Phys Rev E Stat Nonlin Soft Matter Phys. 2005. PMID: 16196611
-
Creep indentation of single cells.J Biomech Eng. 2003 Jun;125(3):334-41. doi: 10.1115/1.1572517. J Biomech Eng. 2003. PMID: 12929237
-
Microviscoelasticity of the apical cell surface of human umbilical vein endothelial cells (HUVEC) within confluent monolayers.Biophys J. 2004 Aug;87(2):1338-50. doi: 10.1529/biophysj.103.037044. Biophys J. 2004. PMID: 15298936 Free PMC article.
-
Microbial surfaces investigated using atomic force microscopy.Biotechnol Prog. 2004 Nov-Dec;20(6):1615-22. doi: 10.1021/bp049742c. Biotechnol Prog. 2004. PMID: 15575691 Review.
-
Stick and grip: measurement systems and quantitative analyses of integrin-mediated cell adhesion strength.Cell Biochem Biophys. 2003;39(1):61-73. doi: 10.1385/CBB:39:1:61. Cell Biochem Biophys. 2003. PMID: 12835529 Review.
Cited by
-
To pull or be pulled: parsing the multiple modes of mechanotransduction.Curr Opin Cell Biol. 2013 Oct;25(5):558-64. doi: 10.1016/j.ceb.2013.06.002. Epub 2013 Jul 2. Curr Opin Cell Biol. 2013. PMID: 23830123 Free PMC article. Review.
-
Stress transmission within the cell.Compr Physiol. 2011 Jan;1(1):499-524. doi: 10.1002/cphy.c100019. Compr Physiol. 2011. PMID: 23737186 Free PMC article. Review.
-
Deformation under flow and morphological recovery of cancer cells.Lab Chip. 2024 Aug 6;24(16):3930-3944. doi: 10.1039/d4lc00246f. Lab Chip. 2024. PMID: 38993177 Free PMC article.
-
Viscoelastic properties of suspended cells measured with shear flow deformation cytometry.Elife. 2022 Sep 2;11:e78823. doi: 10.7554/eLife.78823. Elife. 2022. PMID: 36053000 Free PMC article.
-
Evidence of a large-scale mechanosensing mechanism for cellular adaptation to substrate stiffness.Proc Natl Acad Sci U S A. 2012 May 1;109(18):6933-8. doi: 10.1073/pnas.1117810109. Epub 2012 Apr 16. Proc Natl Acad Sci U S A. 2012. PMID: 22509005 Free PMC article.
References
-
- Albrecht-Buehler, G. 1987. Role of cortical tension in fibroblast shape and movement. Cell Motil. Cytoskeleton. 7:54–67. - PubMed
-
- Balland, M., A. Richert, and F. Gallet. 2005. The dissipative contribution of myosin II in the cytoskeleton dynamics of myoblasts. Eur. Biophys. J. DOI: 10.1007/S00249-004-0447-7. - PubMed
-
- Beil, M., A. Micoulet, G. Von Wichert, S. Paschke, P. Walther, M. B. Omary, P. P. Van Veldhoven, U. Gern, E. Wolff-Hieber, J. Eggermann, J. Waltenberger, G. Adler, et al. 2003. Sphingosylphosphorylcholine regulates keratin network architecture and visco-elastic properties of human cancer cells. Nat. Cell Biol. 9:803–811. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

