Emergent trade-offs and selection for outbreak frequency in spatial epidemics
- PMID: 15604150
- PMCID: PMC539754
- DOI: 10.1073/pnas.0405682101
Emergent trade-offs and selection for outbreak frequency in spatial epidemics
Abstract
Nonspatial theory on pathogen evolution generally predicts selection for maximal number of secondary infections, constrained only by supposed physiological trade-offs between pathogen infectiousness and virulence. Spread of diseases in human populations can, however, exhibit large scale patterns, underlining the need for spatially explicit approaches to pathogen evolution. Here, we show, in a spatial model where all pathogen traits are allowed to evolve independently, that evolutionary trajectories follow a single relationship between transmission and clearance. This trade-off relation is an emergent system property, as opposed to being a property of pathogen physiology, and maximizes outbreak frequency instead of the number of secondary infections. We conclude that spatial pattern formation in contact networks can act to link infectiousness and clearance during pathogen evolution in the absence of any physiological trade-off. Selection for outbreak frequency offers an explanation for the evolution of pathogens that cause mild but frequent infections.
Figures
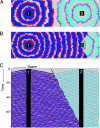
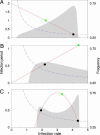
Similar articles
-
Limited role of spatial self-structuring in emergent trade-offs during pathogen evolution.Sci Rep. 2018 Aug 20;8(1):12476. doi: 10.1038/s41598-018-30945-1. Sci Rep. 2018. PMID: 30127509 Free PMC article.
-
Large shifts in pathogen virulence relate to host population structure.Science. 2004 Feb 6;303(5659):842-4. doi: 10.1126/science.1088542. Science. 2004. PMID: 14764881
-
The three Ts of virulence evolution during zoonotic emergence.Proc Biol Sci. 2021 Aug 11;288(1956):20210900. doi: 10.1098/rspb.2021.0900. Epub 2021 Aug 11. Proc Biol Sci. 2021. PMID: 34375554 Free PMC article. Review.
-
Evolution of pathogen virulence across space during an epidemic.Am Nat. 2015 Mar;185(3):332-42. doi: 10.1086/679734. Epub 2015 Jan 28. Am Nat. 2015. PMID: 25674688 Free PMC article.
-
The consequences of spatial structure for the evolution of pathogen transmission rate and virulence.Am Nat. 2009 Oct;174(4):441-54. doi: 10.1086/605375. Am Nat. 2009. PMID: 19691436 Review.
Cited by
-
Griffiths phases and localization in hierarchical modular networks.Sci Rep. 2015 Sep 24;5:14451. doi: 10.1038/srep14451. Sci Rep. 2015. PMID: 26399323 Free PMC article.
-
Evolutionary dynamics of RNA-like replicator systems: A bioinformatic approach to the origin of life.Phys Life Rev. 2012 Sep;9(3):219-63. doi: 10.1016/j.plrev.2012.06.001. Epub 2012 Jun 13. Phys Life Rev. 2012. PMID: 22727399 Free PMC article. Review.
-
Multilevel selection in models of prebiotic evolution II: a direct comparison of compartmentalization and spatial self-organization.PLoS Comput Biol. 2009 Oct;5(10):e1000542. doi: 10.1371/journal.pcbi.1000542. Epub 2009 Oct 16. PLoS Comput Biol. 2009. PMID: 19834556 Free PMC article.
-
Integrating life history and cross-immunity into the evolutionary dynamics of pathogens.Proc Biol Sci. 2006 Feb 22;273(1585):409-16. doi: 10.1098/rspb.2005.3335. Proc Biol Sci. 2006. PMID: 16615206 Free PMC article.
-
Limited role of spatial self-structuring in emergent trade-offs during pathogen evolution.Sci Rep. 2018 Aug 20;8(1):12476. doi: 10.1038/s41598-018-30945-1. Sci Rep. 2018. PMID: 30127509 Free PMC article.
References
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

