Noisy signal amplification in ultrasensitive signal transduction
- PMID: 15625116
- PMCID: PMC544281
- DOI: 10.1073/pnas.0403350102
Noisy signal amplification in ultrasensitive signal transduction
Abstract
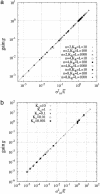
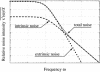
Because intracellular processes are inherently noisy, stochastic reactions process noisy signals in cellular signal transduction. One essential feature of biological signal transduction systems is the amplification of small changes in input signals. However, small random changes in the input signals could also be amplified, and the transduction reaction can also generate noise. Here, we show theoretically how the abrupt response of ultrasensitive signal-transduction reactions results in the generation of large inherent noise and the high amplification of input noise. The inherently generated noise propagates with amplification through intracellular molecular network. We discuss how the contribution of such transmitted noise can be shown experimentally. Our results imply that the switch-like behavior of signal transduction could be limited by noise; however, high amplification reaction could be advantageous to generate large noise, which would be essential to maintain behavioral variability.
Figures


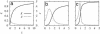
References
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

