Evaluating concentration estimation errors in ELISA microarray experiments
- PMID: 15673468
- PMCID: PMC549203
- DOI: 10.1186/1471-2105-6-17
Evaluating concentration estimation errors in ELISA microarray experiments
Abstract
Background: Enzyme-linked immunosorbent assay (ELISA) is a standard immunoassay to estimate a protein's concentration in a sample. Deploying ELISA in a microarray format permits simultaneous estimation of the concentrations of numerous proteins in a small sample. These estimates, however, are uncertain due to processing error and biological variability. Evaluating estimation error is critical to interpreting biological significance and improving the ELISA microarray process. Estimation error evaluation must be automated to realize a reliable high-throughput ELISA microarray system. In this paper, we present a statistical method based on propagation of error to evaluate concentration estimation errors in the ELISA microarray process. Although propagation of error is central to this method and the focus of this paper, it is most effective only when comparable data are available. Therefore, we briefly discuss the roles of experimental design, data screening, normalization, and statistical diagnostics when evaluating ELISA microarray concentration estimation errors.
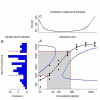
Results: We use an ELISA microarray investigation of breast cancer biomarkers to illustrate the evaluation of concentration estimation errors. The illustration begins with a description of the design and resulting data, followed by a brief discussion of data screening and normalization. In our illustration, we fit a standard curve to the screened and normalized data, review the modeling diagnostics, and apply propagation of error. We summarize the results with a simple, three-panel diagnostic visualization featuring a scatterplot of the standard data with logistic standard curve and 95% confidence intervals, an annotated histogram of sample measurements, and a plot of the 95% concentration coefficient of variation, or relative error, as a function of concentration.
Conclusions: This statistical method should be of value in the rapid evaluation and quality control of high-throughput ELISA microarray analyses. Applying propagation of error to a variety of ELISA microarray concentration estimation models is straightforward. Displaying the results in the three-panel layout succinctly summarizes both the standard and sample data while providing an informative critique of applicability of the fitted model, the uncertainty in concentration estimates, and the quality of both the experiment and the ELISA microarray process.
Figures

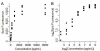
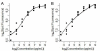

Similar articles
-
In silico microdissection of microarray data from heterogeneous cell populations.BMC Bioinformatics. 2005 Mar 14;6:54. doi: 10.1186/1471-2105-6-54. BMC Bioinformatics. 2005. PMID: 15766384 Free PMC article.
-
A note on using permutation-based false discovery rate estimates to compare different analysis methods for microarray data.Bioinformatics. 2005 Dec 1;21(23):4280-8. doi: 10.1093/bioinformatics/bti685. Epub 2005 Sep 27. Bioinformatics. 2005. PMID: 16188930
-
Predicting protein concentrations with ELISA microarray assays, monotonic splines and Monte Carlo simulation.Stat Appl Genet Mol Biol. 2008;7(1):Article21. doi: 10.2202/1544-6115.1364. Epub 2008 Jul 14. Stat Appl Genet Mol Biol. 2008. PMID: 18673290
-
Multiplexing molecular diagnostics and immunoassays using emerging microarray technologies.Expert Rev Mol Diagn. 2007 Jan;7(1):87-98. doi: 10.1586/14737159.7.1.87. Expert Rev Mol Diagn. 2007. PMID: 17187487 Review.
-
Where statistics and molecular microarray experiments biology meet.Methods Mol Biol. 2013;972:15-35. doi: 10.1007/978-1-60327-337-4_2. Methods Mol Biol. 2013. PMID: 23385529 Review.
Cited by
-
Simultaneous and sensitive detection of six serotypes of botulinum neurotoxin using enzyme-linked immunosorbent assay-based protein antibody microarrays.Anal Biochem. 2012 Nov 15;430(2):185-92. doi: 10.1016/j.ab.2012.08.021. Epub 2012 Aug 27. Anal Biochem. 2012. PMID: 22935296 Free PMC article.
-
Differential Laboratory Diagnosis of Acute Fever in Guinea: Preparedness for the Threat of Hemorrhagic Fevers.Int J Environ Res Public Health. 2021 Jun 3;18(11):6022. doi: 10.3390/ijerph18116022. Int J Environ Res Public Health. 2021. PMID: 34205104 Free PMC article.
-
Application of photonic crystal enhanced fluorescence to cancer biomarker microarrays.Anal Chem. 2011 Feb 15;83(4):1425-30. doi: 10.1021/ac102989n. Epub 2011 Jan 21. Anal Chem. 2011. PMID: 21250635 Free PMC article.
-
Associations Between Follicular Fluid Biomarkers and IVF/ICSI Outcomes in Normo-Ovulatory Women-A Systematic Review.Biomolecules. 2025 Mar 20;15(3):443. doi: 10.3390/biom15030443. Biomolecules. 2025. PMID: 40149979 Free PMC article.
-
Comprehensive Analysis of Cetuximab Critical Quality Attributes: Impact of Handling on Antigen-Antibody Binding.Pharmaceutics. 2024 Sep 19;16(9):1222. doi: 10.3390/pharmaceutics16091222. Pharmaceutics. 2024. PMID: 39339258 Free PMC article.
References
-
- Varnum SM, Woodbury RL, Zangar RC. A protein microarray ELISA for screening biological fluids. Methods Mol Biol. 2004;264:161–172. - PubMed
-
- Racine-Poon A, Weihs C, Smith AFM. Estimation of relative potency with sequential dilution errors in radioim-munoassay. Biometrics. 1991;47:1235–1246. - PubMed
-
- Giltinan DM, Davidian M. Assays for recombinant proteins: a problem in non-linear calibration. Statistics in Medicine. 1994;13:1165–1179. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

