Determination of barrier heights and prefactors from protein folding rate data

Abstract

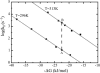
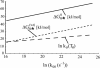
We determine both barrier heights and prefactors for protein folding by applying constraints determined from experimental rate measurements to a Kramers theory for folding rate. The theoretical values are required to match the experimental values at two conditions of temperature and denaturant that induce the same stability. Several expressions for the prefactor in the Kramers rate equation are examined: a random energy approximation, a correlated energy approximation, and an approximation using a single Arrhenius activation energy. Barriers and prefactors are generally found to be large as a result of implementing this recipe, i.e., the folding landscape is cooperative and smooth. Interestingly, a prefactor with a single Arrhenius activation energy admits no formal solution.

FIGURE 1

Logarithm of the rate versus (minus) native stability for horse Cytochrome C, at two temperatures. The plots are well fit by straight line functions that are used in the analysis of the text. Adapted from Mines et al. (1996).

FIGURE 2

Barrier height ΔG_U‡ and prefactors k_o at two temperatures, as obtained from the REM approximation (see text), are plotted as a function of minus stability for cyt-C. The wild-type protein has a stability of ΔG ≈ 74 kJ/mol. Numerical values are given in Table 1. Prefactor attempt rates are in s⁻¹, and barrier heights are in kJ/mol. The short dashed line gives the barrier for a temperature-independent solvent viscosity. All logarithms are natural (base e).

FIGURE 3

(A) The temperature T_G that emerges from the REM analysis for cyt-C (see text and Eq. 16) varies only moderately with barrier height change at constant stability, δ′ΔG_U‡ (the value of which is not known for this protein). For this plot the stability is set to midway between zero and the stability of the wild-type (37 kJ/mol). (B) T_G also changes little as native stability ΔG is varied (for this plot δ′ΔG_U‡ = 0).

FIGURE 4

Barrier heights and prefactors as obtained from the correlated landscape analysis (see text), plotted as a function of minus native stability for h-cyt-C. Numerical values are given in Table 1. Prefactor attempt rates are in s⁻¹, and barrier heights are in kJ/mol. The dotted line gives the barrier for a temperature-independent solvent viscosity. Note prefactors are approximately constant (as is physically reasonable) and solvent viscosity plays a minor role.

FIGURE 5

Barrier heights and prefactors extracted from the recipe for the correlated energy landscape (see text) increase as the bare reconfiguration rate (appearing in Eqs. 17a and 17b) increases. The increase is linear. is the barrier at the transition midpoint, is the barrier at the stability of the wild-type protein, and k_o(T_o) is the prefactor at temperature T_o in s⁻¹.