Immunology and mathematics: crossing the divide
- PMID: 15819694
- PMCID: PMC1782120
- DOI: 10.1111/j.1365-2567.2005.02142.x
Immunology and mathematics: crossing the divide
Abstract
'It's high time molecular biology became quantitative, it cries out to a physicist ... for modeling. Modeling isn't a crutch, it's the opposite; it's a way of suggesting experiments to do, to fill gaps in your understanding.' John Maddox, Editor of Nature 1966-73, and 1980-95.
Figures
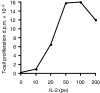
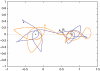

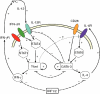
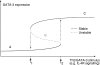


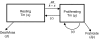

 ) results in a rapid increase in the number of cycling cells and then a slow return of the cycling and resting cells back to the normal equilibrium point (black filled circle). In contrast, in the competition model, addition of Tm cells does not significantly increase the number of cycling cells and the number of resting cells slowly returns back to the equilibrium point (•).
) results in a rapid increase in the number of cycling cells and then a slow return of the cycling and resting cells back to the normal equilibrium point (black filled circle). In contrast, in the competition model, addition of Tm cells does not significantly increase the number of cycling cells and the number of resting cells slowly returns back to the equilibrium point (•).Similar articles
-
Immunoinformatics: a brief review.Methods Mol Biol. 2014;1184:23-55. doi: 10.1007/978-1-4939-1115-8_3. Methods Mol Biol. 2014. PMID: 25048118 Review.
-
An approach to modelling in immunology.Brief Bioinform. 2001 Sep;2(3):245-57. doi: 10.1093/bib/2.3.245. Brief Bioinform. 2001. PMID: 11589585
-
Fine-tuning CD4+ central memory T cell heterogeneity by strength of stimulation.Eur J Immunol. 2008 Jan;38(1):15-9. doi: 10.1002/eji.200738044. Eur J Immunol. 2008. PMID: 18157815 Review.
-
Homeostasis of peripheral immune effectors.Bull Math Biol. 2004 Nov;66(6):1493-514. doi: 10.1016/j.bulm.2004.02.003. Bull Math Biol. 2004. PMID: 15522343
-
The maths of memory.Elife. 2017 Apr 28;6:e26754. doi: 10.7554/eLife.26754. Elife. 2017. PMID: 28453436 Free PMC article.
Cited by
-
Coupled feedback loops form dynamic motifs of cellular networks.Biophys J. 2008 Jan 15;94(2):359-65. doi: 10.1529/biophysj.107.105106. Epub 2007 Oct 19. Biophys J. 2008. PMID: 17951298 Free PMC article.
-
Modeling population heterogeneity from microbial communities to immune response in cells.Cell Mol Life Sci. 2020 Feb;77(3):415-432. doi: 10.1007/s00018-019-03378-w. Epub 2019 Nov 25. Cell Mol Life Sci. 2020. PMID: 31768606 Free PMC article. Review.
-
The Basic Immune Simulator: an agent-based model to study the interactions between innate and adaptive immunity.Theor Biol Med Model. 2007 Sep 27;4:39. doi: 10.1186/1742-4682-4-39. Theor Biol Med Model. 2007. PMID: 17900357 Free PMC article.
-
A systems model for immune cell interactions unravels the mechanism of inflammation in human skin.PLoS Comput Biol. 2010 Dec 2;6(12):e1001024. doi: 10.1371/journal.pcbi.1001024. PLoS Comput Biol. 2010. PMID: 21152006 Free PMC article.
-
Safety of higher dosages of Viscum album L. in animals and humans--systematic review of immune changes and safety parameters.BMC Complement Altern Med. 2011 Aug 28;11:72. doi: 10.1186/1472-6882-11-72. BMC Complement Altern Med. 2011. PMID: 21871125 Free PMC article.
References
-
- Lee KH, Dinner AR, Tu C, et al. The immunological synapse balances T cell receptor signaling and degradation. Science. 2003;302(5648):1218–22. 10.1126/science.1086507. - DOI - PubMed
-
- Germain RN. The art of the probable: system control in the adaptive immune system. Science. 2001;293(5528):240–5. 10.1126/science.1062946. - DOI - PubMed
-
- Macallan DC, Asquith B, Irvine AJ, et al. Measurement and modeling of human T cell kinetics. Eurjimmunol. 2003;33(8):2316–26. - PubMed
-
- Ribeiro RM, Mohri H, Ho DD, Perelson AS. In vivo dynamics of T cell activation, proliferation, and death in HIV-1 infection: Why are CD4+ but not CD8+ T cells depleted? Proc Natl Acad Sci USA. 2002;99(24):15572–7. 10.1073/pnas.242358099. - DOI - PMC - PubMed
-
- Gett AV, Hodgkin PD. A cellular calculus for signal integration by T cells. Nat Immunol. 2000;1(3):239–44. 10.1038/79782. - DOI - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Medical

