Sedimentation velocity analysis of heterogeneous protein-protein interactions: sedimentation coefficient distributions c(s) and asymptotic boundary profiles from Gilbert-Jenkins theory
- PMID: 15863474
- PMCID: PMC1366564
- DOI: 10.1529/biophysj.105.059584
Sedimentation velocity analysis of heterogeneous protein-protein interactions: sedimentation coefficient distributions c(s) and asymptotic boundary profiles from Gilbert-Jenkins theory
Abstract
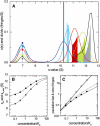
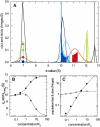
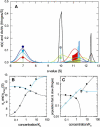
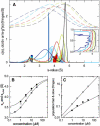
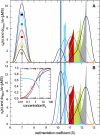
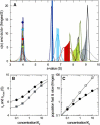
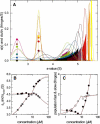
Interacting proteins in rapid association equilibrium exhibit coupled migration under the influence of an external force. In sedimentation, two-component systems can exhibit bimodal boundaries, consisting of the undisturbed sedimentation of a fraction of the population of one component, and the coupled sedimentation of a mixture of both free and complex species in the reaction boundary. For the theoretical limit of diffusion-free sedimentation after infinite time, the shapes of the reaction boundaries and the sedimentation velocity gradients have been predicted by Gilbert and Jenkins. We compare these asymptotic gradients with sedimentation coefficient distributions, c(s), extracted from experimental sedimentation profiles by direct modeling with superpositions of Lamm equation solutions. The overall shapes are qualitatively consistent and the amplitudes and weight-average s-values of the different boundary components are quantitatively in good agreement. We propose that the concentration dependence of the area and weight-average s-value of the c(s) peaks can be modeled by isotherms based on Gilbert-Jenkins theory, providing a robust approach to exploit the bimodal structure of the reaction boundary for the analysis of experimental data. This can significantly improve the estimates for the determination of binding constants and hydrodynamic parameters of the complexes.
Figures


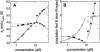

References
-
- Gilbert, G. A., and R. C. Jenkins. 1956. Boundary problems in the sedimentation and electrophoresis of complex systems in rapid reversible equilibrium. Nature. 177:853–854. - PubMed
-
- Gilbert, G. A. 1959. Sedimentation and electrophoresis of interacting substances. I. Idealized boundary shape for a single substance aggregating reversibly. Proc. R. Soc. Lond. A. 250:377–388.
-
- Gilbert, G. A., and R. C. Jenkins. 1959. Sedimentation and electrophoresis of interacting substances. II. Asymptotic boundary shape for two substances interacting reversibly. Proc R. Soc. Lond. A. 253:420–437.
-
- Nichol, L. W., and A. G. Ogston. 1965. A generalized approach to the description of interacting boundaries in migrating systems. Proc. R. Soc. Lond. B Biol. Sci. 163:343–368.
-
- Winzor, D. J., and H. A. Scheraga. 1963. Studies of chemically reacting systems on sephadex. I. Chromatographic demonstration of the Gilbert theory. Biochemistry. 2:1263–1267. - PubMed
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

