Position-sensitive scanning fluorescence correlation spectroscopy

Abstract

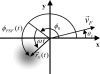
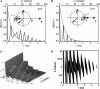
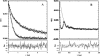
Fluorescence correlation spectroscopy (FCS) uses a stationary laser beam to illuminate a small sample volume and analyze the temporal behavior of the fluorescence fluctuations within the stationary observation volume. In contrast, scanning FCS (SFCS) collects the fluorescence signal from a moving observation volume by scanning the laser beam. The fluctuations now contain both temporal and spatial information about the sample. To access the spatial information we synchronize scanning and data acquisition. Synchronization allows us to evaluate correlations for every position along the scanned trajectory. We use a circular scan trajectory in this study. Because the scan radius is constant, the phase angle is sufficient to characterize the position of the beam. We introduce position-sensitive SFCS (PSFCS), where correlations are calculated as a function of lag time and phase. We present the theory of PSFCS and derive expressions for diffusion, diffusion in the presence of flow, and for immobilization. To test PSFCS we compare experimental data with theory. We determine the direction and speed of a flowing dye solution and the position of an immobilized particle. To demonstrate the feasibility of the technique for applications in living cells we present data of enhanced green fluorescent protein measured in the nucleus of COS cells.

FIGURE 1

Theoretical curves for SFCS for diffusion and diffusion with flow. (A) For the diffusion-only case the FCS autocorrelation function (dashed line) is the envelope of the SFCS curve (solid line). Correlation functions are modeled for τ_D = 1 ms, ρ = 1, and ω = 2πf, where f = 2 kHz. (B) In the presence of flow the SFCS function (solid line) is not enveloped by the FCS correlation function (dashed line). The correlation was calculated for a flow time of τ_F = 1 ms, whereas the other parameters are the same as for panel A.

FIGURE 2

Depiction of the position-sensitive coordinate system. The coordinate system shows how the different angles relevant to the PSF position and the flow vector are defined in a right-handed coordinate system.

FIGURE 3

for flow with (A) For the PSFCS correlation function (solid line) exceeds the FCS autocorrelation (dashed line) when particles had enough time to move from point A to point B (see inset). (B) For the PSFCS autocorrelation curve is enveloped by the FCS autocorrelation curve. Flow transports particles away from point B without ever crossing the scan circumference. The correlation surface as a function of lag time and phase angle is shown (C) along with its contour (D). The flow direction is identified by the fastest decay of the correlation as a function of phase angle. The parameters used for the model are the same as for Fig. 1.

FIGURE 4

SFCS data of a diffusing dye solution. Alexa488 in glycerol solution was scanned at a frequency of 2 kHz and an amplitude of 150 mV. The FCS autocorrelation curve (▵) is the envelope of the SFCS autocorrelation curve (⋄). The fit (solid line) gives ρ = 1.09 ± 0.01 for the scaled radius and a reduced χ² of 1.3. The normalized residuals for fitting the SFCS curve are shown below.

FIGURE 5

SFCS and FCS correlation functions of EGFP at different powers. The dashed line shows the fit to an FCS curve taken with a power of ∼0.5 mW at the sample with a diffusion time of Another FCS measurement of the same sample was taken at a higher power (∼1.75 mW). A fit (solid line) of the correlation function (⋄) to a diffusion model returned an apparent diffusion time of τ_D = 0.15 ± 0.01 ms. The dotted line represents a fit of SFCS data (□) taken at the same power (∼1.75 mW) and determined a diffusion time of The fitted diffusion time as a function of power is shown as an inset. The diffusion time of the FCS measurements (▵) decreases by 30% over the power range studied because of the onset of photobleaching. The diffusion time of SFCS experiments (⋄) on the other hand is significantly more robust.

FIGURE 6

FCS and SFCS flow measurement of an Alexa488 water/glycerol solution. (A) The FCS correlation function (▵) was measured in the absence of flow. Fitting of the data determined a diffusion time of The diamonds represent the FCS correlation function measured in the presence of flow. The fit determined a flow time of The residuals of the fit to the data in the presence of flow are shown below and give a reduced χ² of 1.6. (B) SFCS correlation function (⋄) of the flowing sample was fit to theory. The fit returns a flow time of (reduced χ² = 1.6). The residuals to the fit are graphed below. The dotted line shows the fit to the corresponding FCS correlation function as reference. The SFCS correlation function exceeds the regular FCS function at later times as predicted by theory.

FIGURE 7

PSFCS correlation functions. The experimental correlation functions are only shown for phase angles from 0 to π. The mesh represents the fit of the experimental data to theory. (A) PSFCS correlation function of diffusing Alexa488. The fit of the experimental data to theory determines a diffusion time of The amplitude of the correlation function is independent of phase as expected for diffusion. (B) PSFCS correlation function of Alexa488 flowing inside a capillary. The fit determines a flow angle of with a reduced χ² of 1.6. (B) PSFCS correlation function of Alexa488 with reversed flow direction. Fitting results in a flow angle of (D) PSFCS correlation function of EGFP in vivo. The correlation function is fit by a diffusion-only model with

FIGURE 8

Correlation functions of an immobilized fluorescent sphere. (A) The SFCS correlation function (⋄) is fit to Eq. 26. The fit with a reduced χ² of 1.4 is shown as solid line and determines the radial position of the particle as r_p = 0.35 ± 0.01 μm from the center of the scan. (B) The PSFCS correlation function of the same experiment is shown. Fitting of the data determines both the radial and angular position of the particle; r_p = 0.34 ± 0.01 μm and θ_F = 173.1 ± 0.1° (χ² = 1.4). (C) PSFCS correlation function of the immobilized sphere in the presence of a diffusing dye solution. The periodic peaks characterize the presence of the immobile particle, whereas the decaying, wavelike structure is indicative of the diffusing dye solution. (D) Phase-normalized PSFCS correlation function of the same data as shown in panel C. The periodic peaks of the immobile particle are absent. Fitting of the correlation function to a diffusion-only model yields a reduced χ² of 1.3 with a diffusion time of τ_D = 0.89 ± 0.01 ms.