On the evolutionary stability of Mendelian segregation
- PMID: 15911587
- PMCID: PMC1451198
- DOI: 10.1534/genetics.104.036889
On the evolutionary stability of Mendelian segregation
Abstract
We present a model of a primary locus subject to viability selection and an unlinked locus that causes sex-specific modification of the segregation ratio at the primary locus. If there is a balanced polymorphism at the primary locus, a population undergoing Mendelian segregation can be invaded by modifier alleles that cause sex-specific biases in the segregation ratio. Even though this effect is particularly strong if reciprocal heterozygotes at the primary locus have distinct viabilities, as might occur with genomic imprinting, it also applies if reciprocal heterozygotes have equal viabilities. The expected outcome of the evolution of sex-specific segregation distorters is all-and-none segregation schemes in which one allele at the primary locus undergoes complete drive in spermatogenesis and the other allele undergoes complete drive in oogenesis. All-and-none segregation results in a population in which all individuals are maximally fit heterozygotes. Unlinked modifiers that alter the segregation ratio are unable to invade such a population. These results raise questions about the reasons for the ubiquity of Mendelian segregation.
Figures
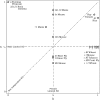
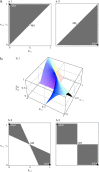
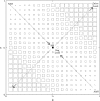
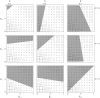

Similar articles
-
Nonrandom segregation during meiosis: the unfairness of females.Mamm Genome. 2001 May;12(5):331-9. doi: 10.1007/s003350040003. Mamm Genome. 2001. PMID: 11331939 Review.
-
Common features of segregation distortion in plants and animals.Genetica. 2003 Jan;117(1):27-35. doi: 10.1023/a:1022308414864. Genetica. 2003. PMID: 12656570
-
Evolution of the segregation ratio: modification of gene conversion and meiotic drive.Theor Popul Biol. 1990 Oct;38(2):192-218. doi: 10.1016/0040-5809(90)90010-s. Theor Popul Biol. 1990. PMID: 2247852
-
Random and non-random mating populations: Evolutionary dynamics in meiotic drive.Math Biosci. 2016 Jan;271:29-41. doi: 10.1016/j.mbs.2015.10.013. Epub 2015 Oct 30. Math Biosci. 2016. PMID: 26524140
-
Why is Mendelian segregation so exact?Bioessays. 1991 Jun;13(6):305-12. doi: 10.1002/bies.950130609. Bioessays. 1991. PMID: 1909864 Review.
Cited by
-
Modeling the Evolution of Female Meiotic Drive in Maize.G3 (Bethesda). 2018 Jan 4;8(1):123-130. doi: 10.1534/g3.117.300073. G3 (Bethesda). 2018. PMID: 29122849 Free PMC article.
-
X-linked meiotic drive can boost population size and persistence.Genetics. 2021 Mar 3;217(1):1-11. doi: 10.1093/genetics/iyaa018. Genetics. 2021. PMID: 33683360 Free PMC article.
-
The evolution of sex-independent transmission ratio distortion involving multiple allelic interactions at a single locus in rice.Genetics. 2008 Sep;180(1):409-20. doi: 10.1534/genetics.108.090126. Epub 2008 Aug 24. Genetics. 2008. PMID: 18723891 Free PMC article.
-
On the origin of sex chromosomes from meiotic drive.Proc Biol Sci. 2015 Jan 7;282(1798):20141932. doi: 10.1098/rspb.2014.1932. Proc Biol Sci. 2015. PMID: 25392470 Free PMC article.
-
A selfish supergene causes meiotic drive through both sexes in Drosophila.Proc Natl Acad Sci U S A. 2025 Apr 29;122(17):e2421185122. doi: 10.1073/pnas.2421185122. Epub 2025 Apr 23. Proc Natl Acad Sci U S A. 2025. PMID: 40267129
References
-
- Agulnik, S. I., A. I. Agulnik and A. O. Ruvinsky, 1990. Meiotic drive in female mice heterozygous for the HSR inserts on chromosome 1. Genet. Res. 55 97–100. - PubMed
-
- Charlesworth, B., 1979. Selection for gamete lethals and s-alleles in complex heterozygotes. Heredity 43 159–164.
-
- Cleland, R. E., 1972 Oenothera Cytogenetics and Evolution. Academic Press, London.
-
- Crow, J. F., 1970 Genetic loads and the cost of natural selection, pp. 128–177 in Mathematical Topics in Population Genetics, edited by K. I. Kojima. Springer-Verlag, New York.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

