Synergy, redundancy, and independence in population codes, revisited
- PMID: 15917459
- PMCID: PMC6724819
- DOI: 10.1523/JNEUROSCI.5319-04.2005
Synergy, redundancy, and independence in population codes, revisited
Abstract
Decoding the activity of a population of neurons is a fundamental problem in neuroscience. A key aspect of this problem is determining whether correlations in the activity, i.e., noise correlations, are important. If they are important, then the decoding problem is high dimensional: decoding algorithms must take the correlational structure in the activity into account. If they are not important, or if they play a minor role, then the decoding problem can be reduced to lower dimension and thus made more tractable. The issue of whether correlations are important has been a subject of heated debate. The debate centers around the validity of the measures used to address it. Here, we evaluate three of the most commonly used ones: synergy, DeltaI(shuffled), and DeltaI. We show that synergy and DeltaI(shuffled) are confounded measures: they can be zero when correlations are clearly important for decoding and positive when they are not. In contrast, DeltaI is not confounded. It is zero only when correlations are not important for decoding and positive only when they are; that is, it is zero only when one can decode exactly as well using a decoder that ignores correlations as one can using a decoder that does not, and it is positive only when one cannot decode as well. Finally, we show that DeltaI has an information theoretic interpretation; it is an upper bound on the information lost when correlations are ignored.
Figures
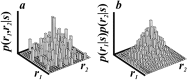


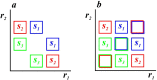

References
-
- Abbott LF, Dayan P (1999) The effect of correlated variability on the accuracy of a population code. Neural Comput 11: 91-101. - PubMed
-
- Atick JJ (1992) Could information theory provide an ecological theory of sensory processing? Network 3: 213-251. - PubMed
-
- Atick JJ, Redlich AN (1990) Towards a theory of early visual processing. Neural Comput 2: 308-320.
-
- Attneave F (1954) Informational aspects of visual perception. Psychol Rev 61: 183-193. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
