Hamilton's indicators of the force of selection
- PMID: 15919822
- PMCID: PMC1140481
- DOI: 10.1073/pnas.0502155102
Hamilton's indicators of the force of selection
Abstract
To quantify the force of selection, Hamilton [Hamilton, W. D. (1966) J. Theor. Biol. 12, 12-45] derived expressions for the change in fitness with respect to age-specific mutations. Hamilton's indicators are decreasing functions of age. He concluded that senescence is inevitable: survival and fertility decline with age. I show that alternative parameterizations of mutational effects lead to indicators that can increase with age. I then consider the case of deleterious mutations with age-specific effects. In this case, it is the balance between mutation and selection pressure that determines the equilibrium number of mutations in a population. In this balance, the effects of different parameterizations cancel out, but only to a linear approximation. I show that mutation accumulation has little impact at ages when this linear approximation holds. When mutation accumulation matters, nonlinear effects become important, and the parameterizations of mutational effects make a difference. The results also suggest that mutation accumulation may be relatively unimportant over most of the reproductive lifespan of any species.
Figures



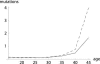
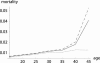

References
-
- Hamilton, W. D. (1966) J. Theor. Biol. 12, 12-45. - PubMed
-
- Hamilton, W. D. (1996) Narrow Roads of Gene Land: The Collected Papers of W. D. Hamilton (Freeman, New York), Vol. 1.
-
- Medawar, P. (1952) An Unsolved Problem of Biology (Lewis, London).
-
- Williams, G. C. (1957) Evolution (Lawrence, Kans.) 11, 398-411.
-
- Lotka, A. J. (1924) Elements of Mathematical Biology; reprinted (1956) (Dover, New York).
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

