Generating quantitative models describing the sequence specificity of biological processes with the stabilized matrix method
- PMID: 15927070
- PMCID: PMC1173087
- DOI: 10.1186/1471-2105-6-132
Generating quantitative models describing the sequence specificity of biological processes with the stabilized matrix method
Abstract
Background: Many processes in molecular biology involve the recognition of short sequences of nucleic-or amino acids, such as the binding of immunogenic peptides to major histocompatibility complex (MHC) molecules. From experimental data, a model of the sequence specificity of these processes can be constructed, such as a sequence motif, a scoring matrix or an artificial neural network. The purpose of these models is two-fold. First, they can provide a summary of experimental results, allowing for a deeper understanding of the mechanisms involved in sequence recognition. Second, such models can be used to predict the experimental outcome for yet untested sequences. In the past we reported the development of a method to generate such models called the Stabilized Matrix Method (SMM). This method has been successfully applied to predicting peptide binding to MHC molecules, peptide transport by the transporter associated with antigen presentation (TAP) and proteasomal cleavage of protein sequences.
Results: Herein we report the implementation of the SMM algorithm as a publicly available software package. Specific features determining the type of problems the method is most appropriate for are discussed. Advantageous features of the package are: (1) the output generated is easy to interpret, (2) input and output are both quantitative, (3) specific computational strategies to handle experimental noise are built in, (4) the algorithm is designed to effectively handle bounded experimental data, (5) experimental data from randomized peptide libraries and conventional peptides can easily be combined, and (6) it is possible to incorporate pair interactions between positions of a sequence.
Conclusion: Making the SMM method publicly available enables bioinformaticians and experimental biologists to easily access it, to compare its performance to other prediction methods, and to extend it to other applications.
Figures

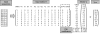



References
-
- Peters B, Bulik S, Tampe R, Van Endert PM, Holzhutter HG. Identifying MHC class I epitopes by predicting the TAP transport efficiency of epitope precursors. J Immunol. 2003;171:1741–1749. - PubMed
-
- Tenzer S, Peters B, Bulik S, Schoor O, Lemmel C, Schatz MM, Kloetzel PM, Rammensee HG, Schild H, Holzhutter HG. Modeling the MHC class I pathway by combining predictions of proteasomal cleavage,TAP transport and MHC class I binding. Cell Mol Life Sci. 2005;62:1025–1037. doi: 10.1007/s00018-005-4528-2. - DOI - PMC - PubMed
-
- Thomason L. TinyXml http://sourceforge.net/projects/tinyxml/
-
- Gnu Scientific Library (GSL) http://www.gnu.org/software/gsl/
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases
Research Materials
Miscellaneous

