Heme regulates allosteric activation of the Slo1 BK channel
- PMID: 15955873
- PMCID: PMC2266614
- DOI: 10.1085/jgp.200509262
Heme regulates allosteric activation of the Slo1 BK channel
Abstract
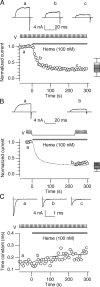
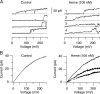
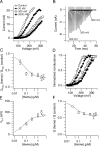
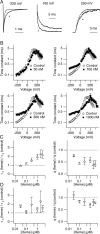
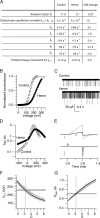
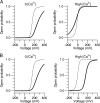
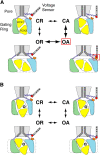
Large conductance calcium-dependent (Slo1 BK) channels are allosterically activated by membrane depolarization and divalent cations, and possess a rich modulatory repertoire. Recently, intracellular heme has been identified as a potent regulator of Slo1 BK channels (Tang, X.D., R. Xu, M.F. Reynolds, M.L. Garcia, S.H. Heinemann, and T. Hoshi. 2003. Nature. 425:531-535). Here we investigated the mechanism of the regulatory action of heme on heterologously expressed Slo1 BK channels by separating the influences of voltage and divalent cations. In the absence of divalent cations, heme generally decreased ionic currents by shifting the channel's G-V curve toward more depolarized voltages and by rendering the curve less steep. In contrast, gating currents remained largely unaffected by heme. Simulations suggest that a decrease in the strength of allosteric coupling between the voltage sensor and the activation gate and a concomitant stabilization of the open state account for the essential features of the heme action in the absence of divalent ions. At saturating levels of divalent cations, heme remained similarly effective with its influence on the G-V simulated by weakening the coupling of both Ca(2+) binding and voltage sensor activation to channel opening. The results thus show that heme dampens the influence of allosteric activators on the activation gate of the Slo1 BK channel. To account for these effects, we consider the possibility that heme binding alters the structure of the RCK gating ring and thereby disrupts both Ca(2+)- and voltage-dependent gating as well as intrinsic stability of the open state.
Figures





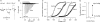
References
-
- Aihara, Y., B.S. Jahromi, R. Yassari, E. Nikitina, M. Agbaje-Williams, and R.L. Macdonald. 2004. Molecular profile of vascular ion channels after experimental subarachnoid hemorrhage. J. Cereb. Blood Flow Metab. 24:75–83. - PubMed
-
- Aldrich, R.W., D.P. Corey, and C.F. Stevens. 1983. A reinterpretation of mammalian sodium channel gating based on single channel recording. Nature. 306:436–441. - PubMed
-
- Armstrong, C.M. 2003. Voltage-gated K channels. Sci STKE. 2003:re10. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Miscellaneous

