DNA knots reveal a chiral organization of DNA in phage capsids

Abstract

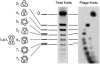
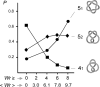
Icosahedral bacteriophages pack their double-stranded DNA genomes to near-crystalline density and achieve one of the highest levels of DNA condensation found in nature. Despite numerous studies, some essential properties of the packaging geometry of the DNA inside the phage capsid are still unknown. We present a different approach to the problems of randomness and chirality of the packed DNA. We recently showed that most DNA molecules extracted from bacteriophage P4 are highly knotted because of the cyclization of the linear DNA molecule confined in the phage capsid. Here, we show that these knots provide information about the global arrangement of the DNA inside the capsid. First, we analyze the distribution of the viral DNA knots by high-resolution gel electrophoresis. Next, we perform Monte Carlo computer simulations of random knotting for freely jointed polygons confined to spherical volumes. Comparison of the knot distributions obtained by both techniques produces a topological proof of nonrandom packaging of the viral DNA. Moreover, our simulations show that the scarcity of the achiral knot 4(1) and the predominance of the torus knot 5(1) over the twist knot 5(2) observed in the viral distribution of DNA knots cannot be obtained by confinement alone but must include writhe bias in the conformation sampling. These results indicate that the packaging geometry of the DNA inside the viral capsid is writhe-directed.

Fig. 1.

Analysis of knotted DNA by gel electrophoresis. (A) DNA was extracted from tailless mutants of phage P4 vir1 del22 and analyzed by two-dimensional agarose gel electrophoresis as described in Materials and Methods. The first dimension at low voltage (top to bottom) separated DNA knot populations according to their crossing number. The unknotted DNA circle or trivial knot (0) has the slowest gel velocity, whereas knotted DNA populations (K) have gel velocity proportional to their crossing number. The second dimension at high voltage (left to right) segregated the linear DNA molecules (L) from the arched distribution of knotted molecules and further resolved some gel bands corresponding to knot subpopulations. (B) Upper area of the gel picture showing knot populations of low crossing number. Individual gel bands corresponding to knot populations containing three to nine crossings are indicated (labeled 3-9) in the main arch of the gel. A second arch of higher gel speed containing knot subpopulations of six and more crossings is generated by the second dimension of the electrophoresis. Individual gel bands of knot subpopulations of six to nine crossings (labeled 6′-9′) are indicated. (C) Quantification of the individual knot populations of six to nine crossings (3-9 and 6′-9′). Both densitometric and phosphorimaging reading of three independent samples of DNA extracted from tailless mutants of phage P4 vir1 del22 produced nearly identical results. The indicated percentage values are relative to the total amount of knotted molecules.

Fig. 2.

Identification of specific knot types by their position in the gel. The gel velocity at low voltage of individual knot populations resolved by two-dimensional electrophoresis (Right) is compared with the gel velocity at low voltage of twist knots (3₁, 4₁, 5₂, 6₁, and 7₂) of a 10-kb nicked plasmid (Center) and with known relative migration distances of some knot types (refs. and 31) (Left). Geometrical representations of the prime knots 3₁, 4₁, 5₁, 5₂, 6₁, 7₁, and 7₂ and of the composite knot 3₁#3₁ are shown. The unknotted DNA circle or trivial knot (0) is also indicated. Note that in the main arch of the two-dimensional gel and below the knots 3₁ and 4₁, the knot population of five crossings matches the migration of the torus knot 5₁, which migrates closer to the knot 4₁ than to the knots of six crossings. The other possible five-crossing knot, the twist knot 5₂, appears to be negligible or absent in the viral distribution. Note also that the knot population of seven crossings matches the migration of the torus knot 7₁ rather than the twist knot 7₂. In the secondary arch of the two-dimensional gel, the first knot population of six crossings has similar low-voltage migration of the composite knot 3₁#3₁.

Fig. 3.

Comparison of experimental and computer-simulated distributions of knots. (A) Distribution probabilities (P(k)) obtained by Monte Carlo simulations of the prime knots 3₁, 4₁, 5₁, and 5₂ for closed ideal polymers of variable chain lengths (n = number of edges) confined to a spherical volume of fixed radius (R = 4 edge lengths). Error bars represent standard deviations. (B) Comparison of the computed probabilities of the knots 3₁, 4₁, 5₁, and 5₂ (for polymers of length n = 90 randomly embedded into a sphere of radius R = 4) with the experimental distribution of knots. The relative amount of each knot type is plotted. Note that fractions of knots 3₁ and 4₁ plausibly formed in free solution are not subtracted from the experimental distribution. If these corrections are considered, the relative amount of knot 4₁ is further reduced.

Fig. 4.

Effect of a writhe-biased sampling on the probability of knots 4₁, 5₁, and 5₂. The writhe of polygons of length n = 90 randomly embedded into a sphere of radius R = 4 were computed, and only conformations whose writhe values were higher than a prefixed value (Wr ≥ 4, 6, or 8) were sampled. The computed mean writhe value () of each sampled population is indicated. The ratios of the probabilities of the knots 4₁, 5₁, and 5₂ relative to that of the knot 3₁ for each writhe-biased sampling are plotted (P).