Mathematical modelling to centre low tidal volumes following acute lung injury: a study with biologically variable ventilation

Abstract

Background: With biologically variable ventilation [BVV--using a computer-controller to add breath-to-breath variability to respiratory frequency (f) and tidal volume (VT)] gas exchange and respiratory mechanics were compared using the ARDSNet low VT algorithm (Control) versus an approach using mathematical modelling to individually optimise VT at the point of maximal compliance change on the convex portion of the inspiratory pressure-volume (P-V) curve (Experimental).

Methods: Pigs (n = 22) received pentothal/midazolam anaesthesia, oleic acid lung injury, then inspiratory P-V curve fitting to the four-parameter logistic Venegas equation F(P) = a + b[1 + e-(P-c)/d]-1 where: a = volume at lower asymptote, b = the vital capacity or the total change in volume between the lower and upper asymptotes, c = pressure at the inflection point and d = index related to linear compliance. Both groups received BVV with gas exchange and respiratory mechanics measured hourly for 5 hrs. Postmortem bronchoalveolar fluid was analysed for interleukin-8 (IL-8).

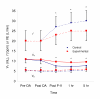
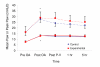
Results: All P-V curves fit the Venegas equation (R2 > 0.995). Control VT averaged 7.4 +/- 0.4 mL/kg as compared to Experimental 9.5 +/- 1.6 mL/kg (range 6.6 - 10.8 mL/kg; p < 0.05). Variable VTs were within the convex portion of the P-V curve. In such circumstances, Jensen's inequality states "if F(P) is a convex function defined on an interval (r, s), and if P is a random variable taking values in (r, s), then the average or expected value (E) of F(P); E(F(P)) > F(E(P))." In both groups the inequality applied, since F(P) defines volume in the Venegas equation and (P) pressure and the range of VTs varied within the convex interval for individual P-V curves. Over 5 hrs, there were no significant differences between groups in minute ventilation, airway pressure, blood gases, haemodynamics, respiratory compliance or IL-8 concentrations.

Conclusion: No difference between groups is a consequence of BVV occurring on the convex interval for individualised Venegas P-V curves in all experiments irrespective of group. Jensen's inequality provides theoretical proof of why a variable ventilatory approach is advantageous under these circumstances. When using BVV, with VT centred by Venegas P-V curve analysis at the point of maximal compliance change, some leeway in low VT settings beyond ARDSNet protocols may be possible in acute lung injury. This study also shows that in this model, the standard ARDSNet algorithm assures ventilation occurs on the convex portion of the P-V curve.

Figure 1

Delivery of Variable Tidal Volume. The complete data set of delivered tidal volume (V_T) using BVV in one animal. There were 376 breaths in the file. Mean V_T was set at 180 mL in this example.

Figure 2

Mathematically Calculated versus Algorithm Low Tidal Volume. V_T calculated from the point of maximal compliance change (c - 1.317d) on the P-V curve for all animals (left hand points) as compared to Control group (ARDSNet algorithm) low V_T (right hand points). Mean V_T of each group given by large open square, connected by the dotted line.

Figure 3

Representative Pressure-Volume Curve Fit to the Venegas Equation. Representative P-V curve generated at zero end expiratory pressure in a single animal in the Experimental group. Dots are individual data points. The line represents the Venegas equation derived P-V curve. The Venegas parameters a, c and b are labelled, as well as the volume at the point of maximal compliance change (P = c - 1.317d) and the volume equivalent to 7 mL/kg in this animal. See text for further explanation.

Figure 4

Frequency Distribution Curves for Tidal Volume for the Two Groups. Frequency distribution curves of V_T for each group calculated in bins of 0.5 mL/kg. The V_T bins are represented on the x-axis and the percentage of all V_Ts from each group in each bin is represented on the y-axis. Control = solid diamonds. Experimental = open squares.

Figure 5

Ventilation Parameter for the Control and Experimental Groups. Mean values of V_T, f, and minute ventilation (V_E) for Control (diamond symbol) and Experimental groups (square symbol) at each time period. Bars represent standard deviation. * p < 0.05 between groups at specified time periods.

Figure 6

Mean Peak and Mean Airway Pressure for the Two Groups. Mean values for peak and mean Paw for Control (diamond) and Experimental (square) groups at each time period. Bars represent standard deviation. *p < 0.05 following oleic acid.