Full cyclic coordinate descent: solving the protein loop closure problem in Calpha space

Abstract

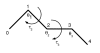
Background: Various forms of the so-called loop closure problem are crucial to protein structure prediction methods. Given an N- and a C-terminal end, the problem consists of finding a suitable segment of a certain length that bridges the ends seamlessly. In homology modelling, the problem arises in predicting loop regions. In de novo protein structure prediction, the problem is encountered when implementing local moves for Markov Chain Monte Carlo simulations. Most loop closure algorithms keep the bond angles fixed or semi-fixed, and only vary the dihedral angles. This is appropriate for a full-atom protein backbone, since the bond angles can be considered as fixed, while the (phi, psi) dihedral angles are variable. However, many de novo structure prediction methods use protein models that only consist of Calpha atoms, or otherwise do not make use of all backbone atoms. These methods require a method that alters both bond and dihedral angles, since the pseudo bond angle between three consecutive Calpha atoms also varies considerably.

Results: Here we present a method that solves the loop closure problem for Calpha only protein models. We developed a variant of Cyclic Coordinate Descent (CCD), an inverse kinematics method from the field of robotics, which was recently applied to the loop closure problem. Since the method alters both bond and dihedral angles, which is equivalent to applying a full rotation matrix, we call our method Full CCD (FCDD). FCCD replaces CCD's vector-based optimization of a rotation around an axis with a singular value decomposition-based optimization of a general rotation matrix. The method is easy to implement and numerically stable.

Conclusion: We tested the method's performance on sets of random protein Calpha segments between 5 and 30 amino acids long, and a number of loops of length 4, 8 and 12. FCCD is fast, has a high success rate and readily generates conformations close to those of real loops. The presence of constraints on the angles only has a small effect on the performance. A reference implementation of FCCD in Python is available as supplementary information.

Figure 1

A protein segment's Cα trace. The Cα positions are numbered, and the pseudo bond angles θ and pseudo dihedrals τ are indicated. The segment has length 5, and is thus fully described by two pseudo dihedral and three pseudo bond angles.

Figure 2

The action of the FCCD algorithm in Cα space. The Cα traces of the moving, fixed and closed segments are shown in red, green and blue, respectively. The Cα atoms are represented as spheres. The labels f₀, f₁ and f₂ indicate the three fixed vectors at the N-terminus that are initially common between the fixed and moving segments. The loop is closed when the three C-terminal vectors of the moving segment (labelled m_N-3, m_N-2, m_N-1) superimpose with an RMSD below the given threshold on the three C-terminal vectors of the fixed segment (labelled (f_N-3, f_N-2, f_N-1). This figure and Figure 3 were made with PyMol .

Figure 3

Loops generated by FCCD (blue) that are close to real protein loops (green). The loops with lowest RMSD to a given loop of length 4 (top), 8 and 12 (bottom) are shown (loops 1qnr, A, 195–198, 3chb, D, 51–58 and 1ctq, A, 26–37). The N- terminus is at the left hand side.