Oblique decision trees for spatial pattern detection: optimal algorithm and application to malaria risk
- PMID: 16026612
- PMCID: PMC1198231
- DOI: 10.1186/1471-2288-5-22
Oblique decision trees for spatial pattern detection: optimal algorithm and application to malaria risk
Abstract
Background: In order to detect potential disease clusters where a putative source cannot be specified, classical procedures scan the geographical area with circular windows through a specified grid imposed to the map. However, the choice of the windows' shapes, sizes and centers is critical and different choices may not provide exactly the same results. The aim of our work was to use an Oblique Decision Tree model (ODT) which provides potential clusters without pre-specifying shapes, sizes or centers. For this purpose, we have developed an ODT-algorithm to find an oblique partition of the space defined by the geographic coordinates.
Methods: ODT is based on the classification and regression tree (CART). As CART finds out rectangular partitions of the covariate space, ODT provides oblique partitions maximizing the interclass variance of the independent variable. Since it is a NP-Hard problem in RN, classical ODT-algorithms use evolutionary procedures or heuristics. We have developed an optimal ODT-algorithm in R2, based on the directions defined by each couple of point locations. This partition provided potential clusters which can be tested with Monte-Carlo inference. We applied the ODT-model to a dataset in order to identify potential high risk clusters of malaria in a village in Western Africa during the dry season. The ODT results were compared with those of the Kulldorff' s SaTScan.
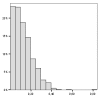
Results: The ODT procedure provided four classes of risk of infection. In the first high risk class 60%, 95% confidence interval (CI95%) [52.22-67.55], of the children was infected. Monte-Carlo inference showed that the spatial pattern issued from the ODT-model was significant (p < 0.0001). Satscan results yielded one significant cluster where the risk of disease was high with an infectious rate of 54.21%, CI95% [47.51-60.75]. Obviously, his center was located within the first high risk ODT class. Both procedures provided similar results identifying a high risk cluster in the western part of the village where a mosquito breeding point was located.
Conclusion: ODT-models improve the classical scanning procedures by detecting potential disease clusters independently of any specification of the shapes, sizes or centers of the clusters.
Figures
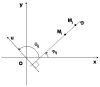
 ; - Mi and Mj are two point locations in the geographical space.
; - Mi and Mj are two point locations in the geographical space.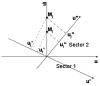
 ; Mi and Mj are two point locations in the geographical space; - Change in the order of the projected coordinates on the u' and u" directions; - u' and u" are directions with intermediate angles, belonging respectively to sector 1 and sector 2; - u'i, u'j, u"i, and u"j are the projected coordinates of points Mi and Mj: u'i > u'j and u"i <u"j.
; Mi and Mj are two point locations in the geographical space; - Change in the order of the projected coordinates on the u' and u" directions; - u' and u" are directions with intermediate angles, belonging respectively to sector 1 and sector 2; - u'i, u'j, u"i, and u"j are the projected coordinates of points Mi and Mj: u'i > u'j and u"i <u"j.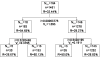

Similar articles
-
Using the SaTScan method to detect local malaria clusters for guiding malaria control programmes.Malar J. 2009 Apr 17;8:68. doi: 10.1186/1475-2875-8-68. Malar J. 2009. PMID: 19374738 Free PMC article.
-
Developing a spatial-statistical model and map of historical malaria prevalence in Botswana using a staged variable selection procedure.Int J Health Geogr. 2007 Sep 24;6:44. doi: 10.1186/1476-072X-6-44. Int J Health Geogr. 2007. PMID: 17892584 Free PMC article.
-
Nonparametric intensity bounds for the delineation of spatial clusters.Int J Health Geogr. 2011 Jan 7;10:1. doi: 10.1186/1476-072X-10-1. Int J Health Geogr. 2011. PMID: 21214924 Free PMC article.
-
Malaria elimination: moving forward with spatial decision support systems.Trends Parasitol. 2012 Jul;28(7):297-304. doi: 10.1016/j.pt.2012.04.002. Epub 2012 May 16. Trends Parasitol. 2012. PMID: 22607693 Review.
-
[Statistical models for spatial analysis in parasitology].Parassitologia. 2004 Jun;46(1-2):75-8. Parassitologia. 2004. PMID: 15305691 Review. Italian.
Cited by
-
Using the SaTScan method to detect local malaria clusters for guiding malaria control programmes.Malar J. 2009 Apr 17;8:68. doi: 10.1186/1475-2875-8-68. Malar J. 2009. PMID: 19374738 Free PMC article.
-
Spatio-temporal patterns and landscape-associated risk of Buruli ulcer in Akonolinga, Cameroon.PLoS Negl Trop Dis. 2014 Sep 4;8(9):e3123. doi: 10.1371/journal.pntd.0003123. eCollection 2014 Sep. PLoS Negl Trop Dis. 2014. PMID: 25188464 Free PMC article.
-
Border analysis for spatial clusters.Int J Health Geogr. 2018 Feb 17;17(1):5. doi: 10.1186/s12942-018-0124-1. Int J Health Geogr. 2018. PMID: 29454357 Free PMC article.
-
Stratification of the severity of critically ill patients with classification trees.BMC Med Res Methodol. 2009 Dec 9;9:83. doi: 10.1186/1471-2288-9-83. BMC Med Res Methodol. 2009. PMID: 20003229 Free PMC article.
-
Malaria in central Vietnam: analysis of risk factors by multivariate analysis and classification tree models.Malar J. 2008 Jan 30;7:28. doi: 10.1186/1475-2875-7-28. Malar J. 2008. PMID: 18234102 Free PMC article.
References
-
- Kulldorff M, Feuer EJ, Miller BA, Freeman LS. Breast cancer in northeastern United States: a geographical analysis. Am J Epidemiol. 1997;146:161–170. - PubMed
-
- Bithell JF. The choice of test for detecting raised disease risk near a point source. Stat Med. 1995;14:2309–2322. - PubMed
-
- Cuzick J, Edwards R. Spatial clustering for inhomogeneous populations. J R Stat Soc [Ser B] 1990;52:73–104.
-
- Tango T. A class of tests for detecting 'general' and 'focused' clustering of rare diseases. Stat Med. 1995;14:2323–2334. - PubMed
-
- Diggle PJ, Morris S, Elliott P, Shaddick G. Regression modelling of disease risk in relation to point sources. J R Stat Soc [Ser A] 1997;160:491–505. doi: 10.1111/1467-985X.00076. - DOI
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical
Research Materials
Miscellaneous

