Geographic routing in social networks

Abstract

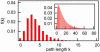
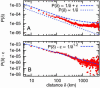
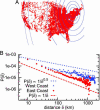
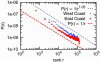
We live in a "small world," where two arbitrary people are likely connected by a short chain of intermediate friends. With scant information about a target individual, people can successively forward a message along such a chain. Experimental studies have verified this property in real social networks, and theoretical models have been advanced to explain it. However, existing theoretical models have not been shown to capture behavior in real-world social networks. Here, we introduce a richer model relating geography and social-network friendship, in which the probability of befriending a particular person is inversely proportional to the number of closer people. In a large social network, we show that one-third of the friendships are independent of geography and the remainder exhibit the proposed relationship. Further, we prove analytically that short chains can be discovered in every network exhibiting the relationship.

Fig. 1.

In-degree (Left) and out-degree (Right) distributions in LiveJournal. For each k, the number N_in(k) of LiveJournal users who are listed as a friend of at least k users and the number N_out(k) of people who list at least k friends are shown, both for all 1,300,000 users and the 500,000 users who list locatable hometowns in the United States.

Fig. 2.

Results of geogreedy on LiveJournal. In each of 500,000 trials, a source s and target t are chosen randomly; at each step, the message is forwarded from the current message-holder u to the friend v of u geographically closest to t.If d(v, t) > d(u, t), then the chain is considered to have failed. The fraction f(k) of pairs in which the chain reaches t's city in exactly k steps is shown (12.78% chains completed; median 4, μ = 4.12, σ = 2.54 for completed chains). (Inset) For 80.16% completed, median 12, μ = 16.74, σ = 17.84; if d(v, t) > d(u, t) then u picks a random person in the same city as u to pass the message to, and the chain fails only if there is no such person available.

Fig. 3.

The relationship between friendship probability and geographic distance. (A) For each distance δ, the proportion P(δ) of friendships among all pairs u, v of LiveJournal users with d(u, v) = δ is shown. Distances are rounded down to multiples of 10 km. The number of pairs u, v with d(u, v) = δ is estimated by computing the distance between 10,000 randomly chosen pairs of people in the network. The curved line corresponding to P(δ) ∝ ε + 1/δ in A models the fact that some LiveJournal friendships are independent of geography: for distances larger than ≈1,000 km, the background friendship probability ε begins to dominate geography-based friendships. (B) The same data are plotted, correcting for the background friendship probability: we plot distance δ versus P(δ) – 5.0 × 10^–6.

Fig. 4.

Evidence of the nonuniformity of the LiveJournal population. (A) A dot is shown for every distinct United States location home to at least one LiveJournal user. The population of each successive displayed circle (all centered on Ithaca, NY) increases by 50,000 people. Note that the gap between the 350,000- and 400,000-person circles encompasses almost the entire Western United States. (B) We show the relationship between friendship probability and geographic distance, as in Fig. 3, restricted to people living on the West Coast (California, Oregon, and Washington) and the East Coast (from Virginia to Maine), respectively.

Fig. 5.

The relationship between friendship probability and rank. The probability P(r) of a link from a randomly chosen source u to the rth closest node to u, that is, the node v such that rank_u(v) = r, in the LiveJournal network, averaged over 10,000 independent source samples. A link from u to one of the nodes S_δ = {v:d(u, v) = δ}, where the people in S_δ are all tied for rank r + 1,..., r +|S_δ|, is counted as a (1/|S_δ|) fraction of a link for each of these ranks. As before, the value of ε represents the background probability of a friendship independent of geography. (A) Data for every 20th rank are shown. Because we do not have fine-grained geographic data, on average the ranks r through r + 1,305 all represent people in the same city; thus we have little data to distinguish among these ranks. (B) The data are averaged into buckets of size 1,306: for each displayed rank r, the average probability of a friendship over ranks {r – 652,..., r + 653} is shown. (C and D) The same data are replotted (unaveraged and averaged, respectively), correcting for the background friendship probability: we plot the rank r versus P(r) – 5.0 × 10^–6.

Fig. 6.

The relationship between friendship probability and rank, as in Fig. 5, restricted to the West and East coasts and averaged over a range of 1,306 ranks.