Morphology of the lamellipodium and organization of actin filaments at the leading edge of crawling cells
- PMID: 16085776
- PMCID: PMC1366852
- DOI: 10.1529/biophysj.105.065383
Morphology of the lamellipodium and organization of actin filaments at the leading edge of crawling cells
Abstract
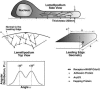
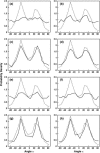
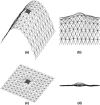
Lamellipodium extension, incorporating actin filament dynamics and the cell membrane, is simulated in three dimensions. The actin filament network topology and the role of actin-associated proteins such as Arp2/3 are examined. We find that the orientational pattern of the filaments is in accord with the experimental data only if the spatial orientation of the Arp2/3 complex is restricted during each branching event. We hypothesize that branching occurs when Arp2/3 is bound to Wiskott-Aldrich syndrome protein (WASP), which is in turn bound to Cdc42 signaling complex; Arp2/3 binding geometry is restricted by the membrane-bound complex. Using mechanical and energetic arguments, we show that any membrane protein that is conical or trapezoidal in shape preferentially resides at the curved regions of the plasma membrane. We hypothesize that the transmembrane receptors involved in the recruitment of Cdc42/WASP complex has this property and concentrate at the leading edge. These features, combined with the mechanical properties of the cell membrane, explain why lamellipodium is a flat organelle.
Figures



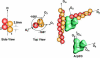

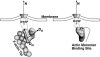


References
-
- Small, J. V., T. Stradal, E. Vignal, and K. Rottner. 2002. The lamellipodium: where motility begins. Trends Cell Biol. 12:112–120. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

