Critical mass hypothesis revisited: role of dynamical wave stability in spontaneous termination of cardiac fibrillation
- PMID: 16113075
- PMCID: PMC3644506
- DOI: 10.1152/ajpheart.00668.2005
Critical mass hypothesis revisited: role of dynamical wave stability in spontaneous termination of cardiac fibrillation
Abstract
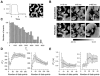
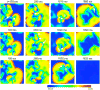
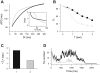
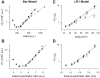
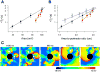
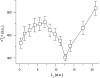
The tendency of atrial or ventricular fibrillation to terminate spontaneously in finite-sized tissue is known as the critical mass hypothesis. Previous studies have shown that dynamical instabilities play an important role in creating new wave breaks that maintain cardiac fibrillation, but its role in self-termination, in relation to tissue size and geometry, is not well understood. This study used computer simulations of two- and three-dimensional tissue models to investigate qualitatively how, in relation to tissue size and geometry, dynamical instability affects the spontaneous termination of cardiac fibrillation. The major findings are as follows: 1) Dynamical instability promotes wave breaks, maintaining fibrillation, but it also causes the waves to extinguish, facilitating spontaneous termination of fibrillation. The latter effect predominates as dynamical instability increases, so that fibrillation is more likely to self-terminate in a finite-sized tissue. 2) In two-dimensional tissue, the average duration of fibrillation increases exponentially as tissue area increases. In three-dimensional tissue, the average duration of fibrillation decreases initially as tissue thickness increases as a result of thickness-induced instability but then increases after a critical thickness is reached. Therefore, in addition to tissue mass and geometry, dynamical instability is an important factor influencing the maintenance of cardiac fibrillation.
Figures
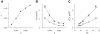
Similar articles
-
Effects of Na(+) and K(+) channel blockade on vulnerability to and termination of fibrillation in simulated normal cardiac tissue.Am J Physiol Heart Circ Physiol. 2005 Oct;289(4):H1692-701. doi: 10.1152/ajpheart.00241.2005. Epub 2005 Jun 3. Am J Physiol Heart Circ Physiol. 2005. PMID: 15937096
-
A simulation study of the effects of cardiac anatomy in ventricular fibrillation.J Clin Invest. 2004 Mar;113(5):686-93. doi: 10.1172/JCI17341. J Clin Invest. 2004. PMID: 14991066 Free PMC article.
-
Induced termination of fibrillation.J Cardiovasc Electrophysiol. 1996 Jan;7(1):71-81. doi: 10.1111/j.1540-8167.1996.tb00462.x. J Cardiovasc Electrophysiol. 1996. PMID: 8718986
-
The dynamics of cardiac fibrillation.Circulation. 2005 Aug 23;112(8):1232-40. doi: 10.1161/CIRCULATIONAHA.104.529545. Circulation. 2005. PMID: 16116073 Review.
-
Additions to the wavelet hypothesis of cardiac fibrillation.J Cardiovasc Electrophysiol. 1994 Jun;5(6):553-9. doi: 10.1111/j.1540-8167.1994.tb01294.x. J Cardiovasc Electrophysiol. 1994. PMID: 8087298 Review.
Cited by
-
Importance of atrial surface area and refractory period in sustaining atrial fibrillation: testing the critical mass hypothesis.J Thorac Cardiovasc Surg. 2013 Sep;146(3):593-8. doi: 10.1016/j.jtcvs.2012.04.021. Epub 2012 Sep 17. J Thorac Cardiovasc Surg. 2013. PMID: 22995722 Free PMC article.
-
Adenosine and Adenosine Receptors: Advances in Atrial Fibrillation.Biomedicines. 2022 Nov 17;10(11):2963. doi: 10.3390/biomedicines10112963. Biomedicines. 2022. PMID: 36428533 Free PMC article. Review.
-
Non-monotonous dose response function of the termination of spiral wave chaos.Sci Rep. 2022 Jul 14;12(1):12043. doi: 10.1038/s41598-022-16068-8. Sci Rep. 2022. PMID: 35835979 Free PMC article.
-
Innovations in Clinical Cardiac Electrophysiology: Challenges and Upcoming Solutions in 2018 and Beyond.J Innov Card Rhythm Manag. 2017 Dec 15;8(12):2943-2955. doi: 10.19102/icrm.2017.081206. eCollection 2017 Dec. J Innov Card Rhythm Manag. 2017. PMID: 32477763 Free PMC article. Review. No abstract available.
-
Nonlinear and Stochastic Dynamics in the Heart.Phys Rep. 2014 Oct 10;543(2):61-162. doi: 10.1016/j.physrep.2014.05.002. Phys Rep. 2014. PMID: 25267872 Free PMC article.
References
-
- Allessie M, Ausma J, Schotten U. Electrical, contractile and structural remodeling during atrial fibrillation. Cardiovasc Res. 2002;54:230–246. - PubMed
-
- Allessie MA, Boyden PA, Camm AJ, Kleber AG, Lab MJ, Legato MJ, Rosen MR, Schwartz PJ, Spooner PM, Van Wagoner DR, Waldo AL. Pathophysiology and prevention of atrial fibrillation. Circulation. 2001;103:769–777. - PubMed
-
- Armoundas AA, Wu R, Juang G, Marban E, Tomaselli GF. Electrical and structural remodeling of the failing ventricle. Pharmacol Ther. 2001;92:213–230. - PubMed
-
- Bar M, Eiswirth M. Turbulence due to spiral breakup in a continuous excitable medium. Phys Rev E. 1993;48:R1635–R1637. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

