Disentangling linkage disequilibrium and linkage from dense single-nucleotide polymorphism trio data
- PMID: 16118185
- PMCID: PMC1456135
- DOI: 10.1534/genetics.105.047431
Disentangling linkage disequilibrium and linkage from dense single-nucleotide polymorphism trio data
Abstract
Parent-offspring trios are widely collected for disease gene-mapping studies and are being extensively genotyped as part of the International HapMap Project. With dense maps of markers on trios, the effects of LD and linkage can be separated, allowing estimation of recombination rates in a model-free setting. Here we define a model-free multipoint method on the basis of dense sequence polymorphism data from parent-offspring trios to estimate intermarker recombination rates. We use simulations to show that this method has up to 92% power to detect recombination hotspots of intensity 25 times background over a region of size 10 kb typed at density 1 marker per 2.5 kb and almost 100% power to detect large hotspots of intensity >125 times background over regions of size 10 kb typed with just 1 marker per 5 kb (alpha = 0.05). We found strong agreement at megabase scales between estimates from our method applied to HapMap trio data and estimates from the genetic map. At finer scales, using Centre d'Etude du Polymorphisme Humain (CEPH) pedigree data across a 10-Mb region of chromosome 20, a comparison of population recombination rate estimates obtained from our method with estimates obtained using a coalescent-based approximate-likelihood method implemented in PHASE 2.0 shows detection of the same coldspots and most hotspots: The Spearman rank correlation between the estimates from our method and those from PHASE is 0.58 (p < 2.2(-16)).
Figures






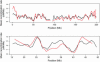
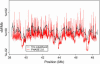
Comment in
-
Estimation of recombination rate and detection of recombination hotspots from dense single-nucleotide polymorphism trio data.Genetics. 2006 Aug;173(4):2415-7. doi: 10.1534/genetics.106.056531. Epub 2006 Jun 18. Genetics. 2006. PMID: 16783018 Free PMC article. No abstract available.
References
-
- Dausset, J., H. Cann, D. Cohen, M. Lahtrop, J. M. Lalouel et al., 1990. Centre d'Etude du Polymorphisme Humain (CEPH): collaborative genetic mapping of the human genome. Genomics 6: 575–577. - PubMed
-
- Devlin, B., N. Risch and S. Roeder, 1996. Disequilibrium mapping: composite likelihood for pairwise disequilibrium. Genomics 36: 1–16. - PubMed
-
- Edwards, A., 1992. Likelihood. John Hopkins University Press, Baltimore.
-
- Efron, B., and R. Tibshirani, 1993. An Introduction to the Bootstrap. Chapman & Hall, London/New York.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials
Miscellaneous

