The solution to the streptavidin-biotin paradox: the influence of history on the strength of single molecular bonds
- PMID: 16169976
- PMCID: PMC1367001
- DOI: 10.1529/biophysj.105.067769
The solution to the streptavidin-biotin paradox: the influence of history on the strength of single molecular bonds
Abstract
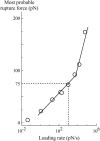
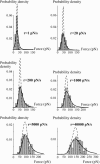
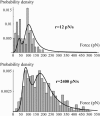
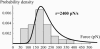
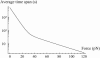
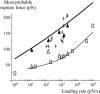
In the past few years, many studies have attempted to measure the strength of a single molecular bond. In general, these experiments consisted in pulling on the bond and measuring the force necessary to dissociate the molecules. However, seemingly contradictory experimental results led to draw the intriguing conclusion that the strength of the bond could depend on the experiment even if the pulling conditions are similar: this paradox was first observed on the widely used streptavidin-biotin bond. Here, by doing supplementary measurements and by reanalyzing the controversial experimental results using Kramers' theory, we show that they can be conciliated. This allows us to show that the strength of a bond is very sensitive to the history of its formation, which is the key to the paradox.
Figures



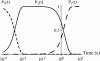

References
-
- Florin, E. L., V. T. Moy, and H. E. Gaub. 1994. Adhesion forces between individual ligand-receptor pairs. Science. 264:415–417. - PubMed
-
- Merkel, R., P. Nassoy, A. Leung, K. Ritchie, and E. Evans. 1999. Energy landscapes of receptor-ligand bonds explored with dynamic force spectroscopy. Nature. 397:50–53. - PubMed
-
- Hanley, W., O. McCarty, S. Jadhav, Y. Tseng, D. Wirtz, and K. Konstantopoulos. 2003. Single molecule characterization of P-selectin/ligand binding. J. Biol. Chem. 278:10556–10561. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

