Müllerian mimicry: an examination of Fisher's theory of gradual evolutionary change
- PMID: 16191639
- PMCID: PMC1560193
- DOI: 10.1098/rspb.2005.3227
Müllerian mimicry: an examination of Fisher's theory of gradual evolutionary change
Abstract
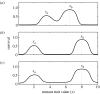
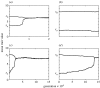
In 1927, Fisher suggested that Müllerian mimicry evolution could be gradual and driven by predator generalization. A competing possibility is the so-called two-step hypothesis, entailing that Müllerian mimicry evolves through major mutational leaps of a less-protected species towards a better-protected, which sets the stage for coevolutionary fine-tuning of mimicry. At present, this hypothesis seems to be more widely accepted than Fisher's suggestion. We conducted individual-based simulations of communities with predators and two prey types to assess the possibility of Fisher's process leading to a common prey appearance. We found that Fisher's process worked for initially relatively similar appearances. Moreover, by introducing a predator spectrum consisting of several predator types with different ranges of generalization, we found that gradual evolution towards mimicry occurred also for large initial differences in prey appearance. We suggest that Fisher's process together with a predator spectrum is a realistic alternative to the two-step hypothesis and, furthermore, it has fewer problems with purifying selection. We also examined the factors influencing gradual evolution towards mimicry and found that not only the relative benefits from mimicry but also the mutational schemes of the prey types matter.
Figures


Similar articles
-
The evolution of Müllerian mimicry.Naturwissenschaften. 2008 Aug;95(8):681-95. doi: 10.1007/s00114-008-0403-y. Epub 2008 Jun 10. Naturwissenschaften. 2008. PMID: 18542902 Free PMC article. Review.
-
Feature theory and the two-step hypothesis of Müllerian mimicry evolution.Evolution. 2010 Mar 1;64(3):810-22. doi: 10.1111/j.1558-5646.2009.00852.x. Epub 2009 Sep 30. Evolution. 2010. PMID: 19796146
-
The evolution of multicomponent mimicry.J Theor Biol. 2007 Feb 21;244(4):631-9. doi: 10.1016/j.jtbi.2006.09.019. Epub 2006 Sep 23. J Theor Biol. 2007. PMID: 17070852
-
Feature saltation and the evolution of mimicry.Evolution. 2012 Mar;66(3):807-817. doi: 10.1111/j.1558-5646.2011.01482.x. Epub 2011 Dec 5. Evolution. 2012. PMID: 22380441
-
Predator perception and the interrelation between different forms of protective coloration.Proc Biol Sci. 2007 Jun 22;274(1617):1457-64. doi: 10.1098/rspb.2007.0220. Proc Biol Sci. 2007. PMID: 17426012 Free PMC article. Review.
Cited by
-
Aposematic signalling in prey-predator systems: determining evolutionary stability when prey populations consist of a single species.J Math Biol. 2022 Jul 23;85(2):13. doi: 10.1007/s00285-022-01762-y. J Math Biol. 2022. PMID: 35870017 Free PMC article.
-
Disentangling taste and toxicity in aposematic prey.Proc Biol Sci. 2012 Dec 19;280(1753):20122588. doi: 10.1098/rspb.2012.2588. Print 2013 Feb 22. Proc Biol Sci. 2012. PMID: 23256198 Free PMC article.
-
The evolution of Müllerian mimicry.Naturwissenschaften. 2008 Aug;95(8):681-95. doi: 10.1007/s00114-008-0403-y. Epub 2008 Jun 10. Naturwissenschaften. 2008. PMID: 18542902 Free PMC article. Review.
-
Generalization of learned preferences covaries with behavioral flexibility in red junglefowl chicks.Behav Ecol. 2019 Sep-Oct;30(5):1375-1381. doi: 10.1093/beheco/arz088. Epub 2019 Jul 13. Behav Ecol. 2019. PMID: 31579147 Free PMC article.
-
Signal categorization by foraging animals depends on ecological diversity.Elife. 2019 Apr 25;8:e43965. doi: 10.7554/eLife.43965. Elife. 2019. PMID: 31021317 Free PMC article.
References
-
- Bates H.W. Contribution to an insect fauna of the Amazon valley. Lepidoptera: Heliconidae. Trans. Linn. Soc. Lond. 1862;23:495–566.
-
- Benson W.W. On the supposed spectrum between Batesian and Müllerian mimicry. Evolution. 1977;31:454–455. - PubMed
-
- Brower L.P, Brower J.V.Z. Parallelism, convergence, divergence, and the new concept of advergence in the evolution of mimicry. Trans. Conn. Acad. Arts Sci. 1972;44:59–67.
-
- Dieckmann U, Law R. The dynamical theory of coevolution: a derivation from stochastic ecological processes. J. Math. Biol. 1996;34:597–612. - PubMed
-
- Fisher R.A. On some objections to mimicry theory; statistical and genetic. Trans. R. Entomol. Soc. 1927;75:269–278.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

