DNA as a programmable viscoelastic nanoelement
- PMID: 16199498
- PMCID: PMC1366951
- DOI: 10.1529/biophysj.105.068866
DNA as a programmable viscoelastic nanoelement
Abstract
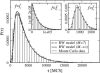
The two strands of a DNA molecule with a repetitive sequence can pair into many different basepairing patterns. For perfectly periodic sequences, early bulk experiments of Pörschke indicate the existence of a sliding process, permitting the rapid transition between different relative strand positions. Here, we use a detailed theoretical model to study the basepairing dynamics of periodic and nearly periodic DNA. As suggested by Pörschke, DNA sliding is mediated by basepairing defects (bulge loops), which can diffuse along the DNA. Moreover, a shear force f on opposite ends of the two strands yields a characteristic dynamic response: An outward average sliding velocity v approximately 1/N is induced in a double strand of length N, provided f is larger than a threshold fc. Conversely, if the strands are initially misaligned, they realign even against an external force f < fc. These dynamics effectively result in a viscoelastic behavior of DNA under shear forces, with properties that are programmable through the choice of the DNA sequence. We find that a small number of mutations in periodic sequences does not prevent DNA sliding, but introduces a time delay in the dynamic response. We clarify the mechanism for the time delay and describe it quantitatively within a phenomenological model. Based on our findings, we suggest new dynamical roles for DNA in artificial nanoscale devices. The basepairing dynamics described here is also relevant for the extension of repetitive sequences inside genomic DNA.
Figures

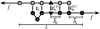




Similar articles
-
Dynamics of force-induced DNA slippage.Phys Rev Lett. 2004 Nov 5;93(19):198102. doi: 10.1103/PhysRevLett.93.198102. Epub 2004 Nov 1. Phys Rev Lett. 2004. PMID: 15600885
-
Intermediate phase in DNA melting.Phys Rev E Stat Nonlin Soft Matter Phys. 2006 Mar;73(3 Pt 1):030902. doi: 10.1103/PhysRevE.73.030902. Epub 2006 Mar 23. Phys Rev E Stat Nonlin Soft Matter Phys. 2006. PMID: 16605493
-
Unzipping of DNA with correlated base sequence.Phys Rev E Stat Nonlin Soft Matter Phys. 2004 Jun;69(6 Pt 1):061908. doi: 10.1103/PhysRevE.69.061908. Epub 2004 Jun 4. Phys Rev E Stat Nonlin Soft Matter Phys. 2004. PMID: 15244618
-
Controlling Matter at the Molecular Scale with DNA Circuits.Annu Rev Biomed Eng. 2019 Jun 4;21:469-493. doi: 10.1146/annurev-bioeng-060418-052357. Annu Rev Biomed Eng. 2019. PMID: 31167101 Review.
-
Enzyme-Free Scalable DNA Digital Design Techniques: A Review.IEEE Trans Nanobioscience. 2016 Dec;15(8):928-938. doi: 10.1109/TNB.2016.2623218. Epub 2016 Dec 2. IEEE Trans Nanobioscience. 2016. PMID: 27925592 Review.
Cited by
-
Force-induced DNA slippage.Biophys J. 2007 Apr 1;92(7):2491-7. doi: 10.1529/biophysj.106.095836. Epub 2007 Jan 11. Biophys J. 2007. PMID: 17218463 Free PMC article.
References
-
- Hagerman, P. J. 1990. Sequence-directed curvature of DNA. Annu. Rev. Biochem. 59:755–781. - PubMed
-
- Widom, J. 2001. Role of DNA sequence in nucleosome stability and dynamics. Q. Rev. Biophys. 34:269–324. - PubMed
-
- Rippe, K., P. H. von Hippel, and J. Langowski. 1995. Action at a distance: DNA-looping and initiation of transcription. Trends Biochem. Sci. 20:500–506. - PubMed
-
- Seeman, N. C. 2003. DNA in a material world. Nature. 421:427–431. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Research Materials

