Mechanisms of excitation-contraction coupling in an integrative model of the cardiac ventricular myocyte
- PMID: 16214852
- PMCID: PMC1367039
- DOI: 10.1529/biophysj.105.065169
Mechanisms of excitation-contraction coupling in an integrative model of the cardiac ventricular myocyte
Abstract
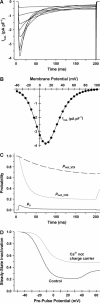
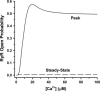
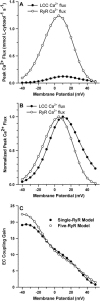
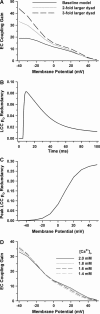
It is now well established that characteristic properties of excitation-contraction (EC) coupling in cardiac myocytes, such as high gain and graded Ca(2+) release, arise from the interactions that occur between L-type Ca(2+) channels (LCCs) and nearby ryanodine-sensitive Ca(2+) release channels (RyRs) in localized microdomains. Descriptions of Ca(2+)-induced Ca(2+) release (CICR) that account for these local mechanisms are lacking from many previous models of the cardiac action potential, and those that do include local control of CICR are able to reconstruct properties of EC coupling, but require computationally demanding stochastic simulations of approximately 10(5) individual ion channels. In this study, we generalize a recently developed analytical approach for deriving simplified mechanistic models of CICR to formulate an integrative model of the canine cardiac myocyte which is computationally efficient. The resulting model faithfully reproduces experimentally measured properties of EC coupling and whole cell phenomena. The model is used to study the role of local redundancy in L-type Ca(2+) channel gating and the role of dyad configuration on EC coupling. Simulations suggest that the characteristic steep rise in EC coupling gain observed at hyperpolarized potentials is a result of increased functional coupling between LCCs and RyRs. We also demonstrate mechanisms by which alterations in the early repolarization phase of the action potential, resulting from reduction of the transient outward potassium current, alters properties of EC coupling.
Figures


Similar articles
-
An integrative model of the cardiac ventricular myocyte incorporating local control of Ca2+ release.Biophys J. 2002 Dec;83(6):2918-45. doi: 10.1016/S0006-3495(02)75301-0. Biophys J. 2002. PMID: 12496068 Free PMC article.
-
A simplified local control model of calcium-induced calcium release in cardiac ventricular myocytes.Biophys J. 2004 Dec;87(6):3723-36. doi: 10.1529/biophysj.104.049973. Epub 2004 Oct 1. Biophys J. 2004. PMID: 15465866 Free PMC article.
-
A human ventricular myocyte model with a refined representation of excitation-contraction coupling.Biophys J. 2015 Jul 21;109(2):415-27. doi: 10.1016/j.bpj.2015.06.017. Biophys J. 2015. PMID: 26200878 Free PMC article.
-
[Microscopic mechanism of excitation-contraction coupling in cardiac myocytes].Sheng Li Ke Xue Jin Zhan. 2004 Oct;35(4):294-8. Sheng Li Ke Xue Jin Zhan. 2004. PMID: 15727204 Review. Chinese.
-
Bridging the myoplasmic gap: recent developments in skeletal muscle excitation-contraction coupling.J Muscle Res Cell Motil. 2007;28(4-5):275-83. doi: 10.1007/s10974-007-9118-5. Epub 2007 Sep 26. J Muscle Res Cell Motil. 2007. PMID: 17899404 Review.
Cited by
-
The relative contributions of store-operated and voltage-gated Ca2+ channels to the control of Ca2+ oscillations in airway smooth muscle.J Physiol. 2017 May 15;595(10):3129-3141. doi: 10.1113/JP272996. Epub 2016 Sep 21. J Physiol. 2017. PMID: 27502470 Free PMC article.
-
A bilobal model of Ca2+-dependent inactivation to probe the physiology of L-type Ca2+ channels.J Gen Physiol. 2018 Dec 3;150(12):1688-1701. doi: 10.1085/jgp.201812115. Epub 2018 Nov 23. J Gen Physiol. 2018. PMID: 30470716 Free PMC article.
-
A kinetic model for calcium dynamics in RAW 264.7 cells: 1. Mechanisms, parameters, and subpopulational variability.Biophys J. 2007 Aug 1;93(3):709-28. doi: 10.1529/biophysj.106.097469. Epub 2007 May 4. Biophys J. 2007. PMID: 17483174 Free PMC article.
-
A probability density approach to modeling local control of calcium-induced calcium release in cardiac myocytes.Biophys J. 2007 Apr 1;92(7):2311-28. doi: 10.1529/biophysj.106.099861. Epub 2007 Jan 19. Biophys J. 2007. PMID: 17237200 Free PMC article.
-
Phospholemman is a negative feed-forward regulator of Ca2+ in β-adrenergic signaling, accelerating β-adrenergic inotropy.J Mol Cell Cardiol. 2012 May;52(5):1048-55. doi: 10.1016/j.yjmcc.2011.12.015. Epub 2012 Jan 20. J Mol Cell Cardiol. 2012. PMID: 22289214 Free PMC article.
References
-
- Cannell, M., J. Berlin, and W. Lederer. 1987. Effect of membrane potential changes on the calcium transient in single rat cardiac muscle cells. Science. 283:1419–1423. - PubMed
-
- Nabauer, M., G. Gallewaert, L. Cleeman, and M. Morad. 1989. Regulation of calcium release is gated by calcium current, not gating charge, in cardiac myocytes. Science. 244:800–803. - PubMed
-
- Cheng, H., W. J. Lederer, and M. B. Cannell. 1993. Calcium sparks: elementary events underlying excitation-contraction coupling in heart muscle. Science. 262:740–744. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases
Miscellaneous

