Dipolar coupling between nitroxide spin labels: the development and application of a tether-in-a-cone model
- PMID: 16214868
- PMCID: PMC1367032
- DOI: 10.1529/biophysj.105.068544
Dipolar coupling between nitroxide spin labels: the development and application of a tether-in-a-cone model
Abstract
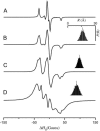
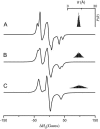
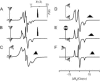
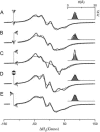
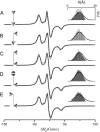
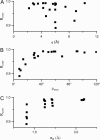
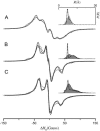
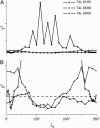
A tether-in-a-cone model is developed for the simulation of electron paramagnetic resonance spectra of dipolar coupled nitroxide spin labels attached to tethers statically disordered within cones of variable halfwidth. In this model, the nitroxides adopt a range of interprobe distances and orientations. The aim is to develop tools for determining both the distance distribution and the relative orientation of the labels from experimental spectra. Simulations demonstrate the sensitivity of electron paramagnetic resonance spectra to the orientation of the cones as a function of cone halfwidth and other parameters. For small cone halfwidths (< approximately 40 degrees ), simulated spectra are strongly dependent on the relative orientation of the cones. For larger cone halfwidths, spectra become independent of cone orientation. Tether-in-a-cone model simulations are analyzed using a convolution approach based on Fourier transforms. Spectra obtained by the Fourier convolution method more closely fit the tether-in-a-cone simulations as the halfwidth of the cone increases. The Fourier convolution method gives a reasonable estimate of the correct average distance, though the distance distribution obtained can be significantly distorted. Finally, the tether-in-a-cone model is successfully used to analyze experimental spectra from T4 lysozyme. These results demonstrate the utility of the model and highlight directions for further development.
Figures






Similar articles
-
Structural refinement from restrained-ensemble simulations based on EPR/DEER data: application to T4 lysozyme.J Phys Chem B. 2013 May 2;117(17):4740-54. doi: 10.1021/jp311723a. Epub 2013 Apr 11. J Phys Chem B. 2013. PMID: 23510103 Free PMC article.
-
A multifrequency electron spin resonance study of T4 lysozyme dynamics.Biophys J. 1999 Jun;76(6):3298-306. doi: 10.1016/S0006-3495(99)77482-5. Biophys J. 1999. PMID: 10354455 Free PMC article.
-
Trajectory-Based Simulation of EPR Spectra: Models of Rotational Motion for Spin Labels on Proteins.J Phys Chem B. 2019 Dec 5;123(48):10131-10141. doi: 10.1021/acs.jpcb.9b02693. Epub 2019 Nov 21. J Phys Chem B. 2019. PMID: 31693365 Free PMC article.
-
Nitroxide spin-spin interactions: applications to protein structure and dynamics.Annu Rev Biophys Biomol Struct. 1999;28:129-53. doi: 10.1146/annurev.biophys.28.1.129. Annu Rev Biophys Biomol Struct. 1999. PMID: 10410798 Review.
-
Conformational dynamics and distribution of nitroxide spin labels.Prog Nucl Magn Reson Spectrosc. 2013 Jul;72:42-60. doi: 10.1016/j.pnmrs.2013.03.001. Epub 2013 Apr 18. Prog Nucl Magn Reson Spectrosc. 2013. PMID: 23731861 Review.
Cited by
-
Navigating Membrane Protein Structure, Dynamics, and Energy Landscapes Using Spin Labeling and EPR Spectroscopy.Methods Enzymol. 2015;564:349-87. doi: 10.1016/bs.mie.2015.07.026. Epub 2015 Aug 29. Methods Enzymol. 2015. PMID: 26477257 Free PMC article.
-
Distance measurements on a dual-labeled TOAC AChR M2δ peptide in mechanically aligned DMPC bilayers via dipolar broadening CW-EPR spectroscopy.J Phys Chem B. 2012 Mar 29;116(12):3866-73. doi: 10.1021/jp212272d. Epub 2012 Mar 19. J Phys Chem B. 2012. PMID: 22379959 Free PMC article.
-
Determination of structural models of the complex between the cytoplasmic domain of erythrocyte band 3 and ankyrin-R repeats 13-24.J Biol Chem. 2011 Jun 10;286(23):20746-57. doi: 10.1074/jbc.M111.230326. Epub 2011 Apr 14. J Biol Chem. 2011. PMID: 21493712 Free PMC article.
-
Electron Paramagnetic Resonance as a Tool for Studying Membrane Proteins.Biomolecules. 2020 May 13;10(5):763. doi: 10.3390/biom10050763. Biomolecules. 2020. PMID: 32414134 Free PMC article. Review.
-
Retinal guanylyl cyclase activating protein 1 forms a functional dimer.PLoS One. 2018 Mar 7;13(3):e0193947. doi: 10.1371/journal.pone.0193947. eCollection 2018. PLoS One. 2018. PMID: 29513743 Free PMC article.
References
-
- Hubbell, W. L., and C. Altenbach. 1994. Investigation of structure and dynamics in membrane proteins using site-directed spin-labeling. Curr. Opin. Struct. Biol. 4:566–573.
-
- Hubbell, W. L., D. S. Cafiso, and C. Altenbach. 2000. Identifying conformational changes with site-directed spin labeling. Nat. Struct. Biol. 7:735–739. - PubMed
-
- Mchaourab, H. S., and E. Perozo. 2000. Determination of protein folds and conformational dynamics using spin-labeling EPR spectroscopy. In Biological Magnetic Resonance: Distance Measurements in Biological Systems by EPR, Vol. 19. L. J. Berliner, G. R. Eaton, and S. S. Eaton, editors. Kluwer Academic/Plenum Publishers, New York, NY. 185–247.
-
- Hustedt, E. J., and A. H. Beth. 1999. Nitroxide spin-spin interactions: applications to protein structure and dynamics. Annu. Rev. Biophys. Biomol. Struct. 28:129–153. - PubMed
-
- Columbus, L., and W. L. Hubbell. 2002. A new spin on protein dynamics. Trends Biochem. Sci. 27:288–295. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

