Making ATP
- PMID: 16217018
- PMCID: PMC1283826
- DOI: 10.1073/pnas.0507207102
Making ATP
Abstract
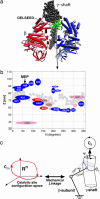
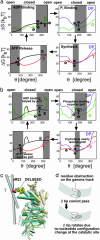
We present a mesoscopic model for ATP synthesis by F(1)F(o) ATPase. The model combines the existing experimental knowledge of the F(1) enzyme into a consistent mathematical model that illuminates how the stages in synthesis are related to the protein structure. For example, the model illuminates how specific interactions between the gamma, epsilon, and alpha(3)beta(3) subunits couple the F(o) motor to events at the catalytic sites. The model also elucidates the origin of ADP inhibition of F(1) in its hydrolysis mode. The methodology we develop for constructing the structure-based model should prove useful in modeling other protein motors.
Figures
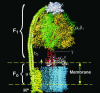


Similar articles
-
Covalent modification of the catalytic sites of the H(+)-ATPase from chloroplasts, CF(0)F(1), with 2-azido-[alpha-(32)P]ADP: modification of the catalytic site 2 (loose) and the catalytic site 3 (open) impairs multi-site, but not uni-site catalysis of both ATP synthesis and ATP hydrolysis.Biochim Biophys Acta. 2000 Jan 10;1456(2-3):77-98. doi: 10.1016/s0005-2728(99)00106-1. Biochim Biophys Acta. 2000. PMID: 10627297
-
Modulation of nucleotide binding to the catalytic sites of thermophilic F(1)-ATPase by the epsilon subunit: implication for the role of the epsilon subunit in ATP synthesis.Biochem Biophys Res Commun. 2009 Dec 11;390(2):230-4. doi: 10.1016/j.bbrc.2009.09.092. Epub 2009 Sep 26. Biochem Biophys Res Commun. 2009. PMID: 19785990
-
Covalent modification of the non-catalytic sites of the H(+)-ATPase from chloroplasts with 2-azido-[alpha-(32)P]ATP and its effect on ATP synthesis and ATP hydrolysis.Biochim Biophys Acta. 2001 Feb 9;1510(1-2):378-400. doi: 10.1016/s0005-2736(00)00371-0. Biochim Biophys Acta. 2001. PMID: 11342174
-
ATP synthase: what we know about ATP hydrolysis and what we do not know about ATP synthesis.Biochim Biophys Acta. 2000 May 31;1458(2-3):300-9. doi: 10.1016/s0005-2728(00)00082-7. Biochim Biophys Acta. 2000. PMID: 10838046 Review.
-
Does the gamma subunit move to an abortive position of ATP hydrolysis when the F1.ADP.Mg complex isomerizes to the inactive F1*.ADP.Mg complex?J Bioenerg Biomembr. 1996 Oct;28(5):433-8. doi: 10.1007/BF02113985. J Bioenerg Biomembr. 1996. PMID: 8951090 Review.
Cited by
-
Biophysical comparison of ATP synthesis mechanisms shows a kinetic advantage for the rotary process.Proc Natl Acad Sci U S A. 2016 Oct 4;113(40):11220-11225. doi: 10.1073/pnas.1608533113. Epub 2016 Sep 19. Proc Natl Acad Sci U S A. 2016. PMID: 27647911 Free PMC article.
-
Extending the absorbing boundary method to fit dwell-time distributions of molecular motors with complex kinetic pathways.Proc Natl Acad Sci U S A. 2007 Feb 27;104(9):3171-6. doi: 10.1073/pnas.0611519104. Epub 2007 Feb 21. Proc Natl Acad Sci U S A. 2007. PMID: 17360624 Free PMC article.
-
Dwell time symmetry in random walks and molecular motors.Biophys J. 2007 Jun 1;92(11):3804-16. doi: 10.1529/biophysj.106.103044. Epub 2007 Mar 16. Biophys J. 2007. PMID: 17369422 Free PMC article. Review.
-
Profile of George Oster.Proc Natl Acad Sci U S A. 2006 Feb 7;103(6):1672-4. doi: 10.1073/pnas.0509056103. Epub 2006 Jan 30. Proc Natl Acad Sci U S A. 2006. PMID: 16446440 Free PMC article. No abstract available.
-
Invadolysin, a conserved lipid-droplet-associated metalloproteinase, is required for mitochondrial function in Drosophila.J Cell Sci. 2013 Oct 15;126(Pt 20):4769-81. doi: 10.1242/jcs.133306. Epub 2013 Aug 13. J Cell Sci. 2013. PMID: 23943867 Free PMC article.
References
-
- Boyer, P. (1997) Annu. Rev. Biochem. 66, 717–749. - PubMed
-
- Kinosita, K., Adachi, K. & Itoh, H. (2004) Annu. Rev. Biophys. Biomol. Struct. 33, 245–268. - PubMed
-
- Nakamoto, R., Ketchum, C., Kuo, P., Peskova, Y. & Al-Shawi, M. (2000) Biochim. Biophys. Acta 1458, 289–299. - PubMed
-
- Weber, J. & Senior, A. E. (2003) FEBS Lett. 545, 61–70. - PubMed
-
- Weber, J. & Senior, A. (2000) Biochim. Biophys. Acta 1458, 300–309. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

