Support from the relationship of genetic and geographic distance in human populations for a serial founder effect originating in Africa
- PMID: 16243969
- PMCID: PMC1276087
- DOI: 10.1073/pnas.0507611102
Support from the relationship of genetic and geographic distance in human populations for a serial founder effect originating in Africa
Abstract
Equilibrium models of isolation by distance predict an increase in genetic differentiation with geographic distance. Here we find a linear relationship between genetic and geographic distance in a worldwide sample of human populations, with major deviations from the fitted line explicable by admixture or extreme isolation. A close relationship is shown to exist between the correlation of geographic distance and genetic differentiation (as measured by F(ST)) and the geographic pattern of heterozygosity across populations. Considering a worldwide set of geographic locations as possible sources of the human expansion, we find that heterozygosities in the globally distributed populations of the data set are best explained by an expansion originating in Africa and that no geographic origin outside of Africa accounts as well for the observed patterns of genetic diversity. Although the relationship between F(ST) and geographic distance has been interpreted in the past as the result of an equilibrium model of drift and dispersal, simulation shows that the geographic pattern of heterozygosities in this data set is consistent with a model of a serial founder effect starting at a single origin. Given this serial-founder scenario, the relationship between genetic and geographic distance allows us to derive bounds for the effects of drift and natural selection on human genetic variation.
Figures


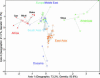

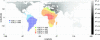
References
-
- Malécot, G. (1991) The Mathematics of Heredity (Freeman, San Francisco).
-
- Cavalli-Sforza, L. L., Barrai, I. & Edwards, A. W. F. (1964) Cold Spring Harbor Symp. Quant. Biol. 29, 9-20. - PubMed
-
- Wijsman, E. M. & Cavalli-Sforza, L. L. (1984) Annu. Rev. Ecol. Syst. 15, 279-301.
-
- Morton, N. E. (1973) in Genetic Structure of Populations, ed. Morton, N. E. (Univ. Press of Hawaii, Honolulu), pp. 76-79.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

