Catch-bond model derived from allostery explains force-activated bacterial adhesion

Abstract

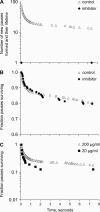
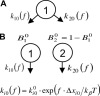
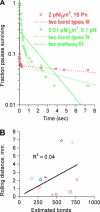
High shear enhances the adhesion of Escherichia coli bacteria binding to mannose coated surfaces via the adhesin FimH, raising the question as to whether FimH forms catch bonds that are stronger under tensile mechanical force. Here, we study the length of time that E. coli pause on mannosylated surfaces and report a double exponential decay in the duration of the pauses. This double exponential decay is unlike previous single molecule or whole cell data for other catch bonds, and indicates the existence of two distinct conformational states. We present a mathematical model, derived from the common notion of chemical allostery, which describes the lifetime of a catch bond in which mechanical force regulates the transitions between two conformational states that have different unbinding rates. The model explains these characteristics of the data: a double exponential decay, an increase in both the likelihood and lifetime of the high-binding state with shear stress, and a biphasic effect of force on detachment rates. The model parameters estimated from the data are consistent with the force-induced structural changes shown earlier in FimH. This strongly suggests that FimH forms allosteric catch bonds. The model advances our understanding of both catch bonds and the role of allostery in regulating protein activity.

FIGURE 1

Pause lifetimes of E. coli bound to mannose-BSA coated surfaces. (A) Locations of several bacteria as a function of time for a medium shear stress of 0.5 pN/μm², showing short and long pauses. (B) Fraction of measured pauses lasting at least the indicated length of time at low (0.01 pN/μm²; ⋄) and high (2 pN/μm²; □) shear. The lines shown in this figure are a fit with a double exponential decay model and give a ∼70-fold (low shear) and ∼360-fold (high shear) difference between the fast and slow decay rates.

FIGURE 2

Tests for whether single bonds cause the pauses. (A) Soluble inhibitor prevents new pauses. In the control experiment without inhibitor (▵), many new pauses began at medium shear stress (0.5 pN/μm²). In the presence of 5% α-methyl mannoside inhibitor (♦), only one new pause began. These results are normalized for the number of bacteria moving in the field of view. This indicates that the inhibitor prevented new bonds from forming. (B) Effect of soluble inhibitor on the lifetime of preexisting pauses in the same experiment as in panel A. The presence (•) or absence (▵) of 5% α-methyl mannoside inhibitor does not effect the distribution of preexisting pause lifetimes at medium shear stress (0.5 pN/μm²). No effect of inhibitor on pause lifetime is observed. (You may notice that both conditions in this experiment show a higher fraction of long pauses relative to other experiments in this article. This is because we normally counted all pauses that started in a set interval, but could not do so in this experiment because inhibitor prevents new pauses from beginning. Here we instead counted all pauses that already existed at the moment when new solution entered the chamber. Using existing pauses oversamples the long pauses. Nevertheless, this experiment is valid to compare the inhibitor with the control because both were measured the same way.) (C) Effect of changing the concentration of receptor on the surface at.0.26 pN/μm². This was achieved by reducing the concentration of mannose-BSA in the incubation from 200 (▵) to 20 (▪) μg/ml, and resulted in ∼10-fold fewer pauses. The data here is expressed as fraction of total pauses measured, so that the difference in total pause number is not seen in the figure except as a difference in the number of nonredundant data points. Changing the receptor concentration also had no significant effect on the distribution of pause lifetimes.

FIGURE 3

Energy landscape of an allosteric catch-bond model and the associated rate constants. (A) Projections of the energy landscapes onto the direction of applied force, for the three transitions involved. The allosteric transition between state 1 (weak) and state 2 (strong) is shown as a dotted line. Unbinding transitions from states 1 or 2 are shown as solid lines. The unbound state(s) are not shown because our model doesn't assume whether there are one, two, or more unbound states, nor does our data analysis probe this part of the energy landscape. The x-dimension in this illustration can be viewed as the extension of the receptor-ligand complex. Each is the height of the energy barrier, whereas each is the transition state distance (the projection of the vector from state i to the transition state to j onto the force vector). (B) The two-state model used to represent this energy landscape.

FIGURE 4

The allosteric catch-bond model fit to the length of time bacteria pause. (A) The fraction of pauses surviving is graphed as a function of the time since each pause started, for a shear stress of 0.01 pN/μm² (green diamonds), 0.5 pN/μm² (blue triangles), 1 pN/μm² (magenta circles), and 2 pN/μm² (red squares). The model was fit using SAAM II software as described in the Materials and Methods section, and the parameters of this fit are given in Table 1. The results for 0.05 and 0.26 pN/μm² are not shown in the figure to avoid cluttering. The triplicate experiments are shown as three sizes of symbols, and the model predictions as lines. At each force, the model predicts a double exponential decay in bond survival: (Eq. 5). The model behavior can be understood from how force affects the two lifetimes 1/ and 1/ (C, dashed and dotted lines), and their coefficients C₁ and C₂ (B, dashed and dotted lines), because all are derived parameters of force and the eight parameters of Table 1). The overall mean lifetime is shown in panel C by the heavy solid line.

FIGURE 5

Testing predictions of the allosteric catch-bond model. (A) Behavior at higher shear stress for the allosteric model. The black diamonds show the new pause survival data at 10.9 pN/μm². The thin black line shows the predicted model behavior at 90 pN (10.9 pN/μm²) with the parameters in Table 1, and the thin dashed and dotted lines show the prediction with mean − 1 SD decrease in k₂₀⁰ and x₂₀, respectively. The thick black line shows a good fit of the data with = 1.37 Å or = 0.0033 s⁻¹ and is within the predicted range. The colored lines show the model fit for the shear conditions of Fig. 3. (B) Bond number as a predictor of distance rolled for the allosteric model. The total number of bonds was estimated for each video as the normalization factor required to fit the models to the data. The distance the bacteria rolled was directly measured by tracking the bacteria in the videos. The bond number is approximately proportional to the distance rolled, (R² = 0.8).

FIGURE 6

Real-time response to changes in shear stress. Bacteria were bound at 0.2 pN/μm², unbound bacteria were washed away, and then bacteria were switched from moderate (0.2 pN/μm²) to high (2 pN/μm²) and then back to low (0.01 pN/μm²) shear stress at times indicated by the dotted vertical lines. (A) Sample trajectories of individual bacteria are shown. The bacteria stopped moving almost immediately when the shear was turned up. However, each bacterium waited a longer time before beginning to move again when the shear was turned back down. (B) The total number of moving bacteria is reported at each time point. Bacteria are defined as moving if they move at any time over the next 1 s, because the short-lived pauses generally lasted <1 s. At each change in shear, the data is fit to get a transition rate between moving and stationary behavior (solid gray line). The rates obtained in this fit are 4.9 s⁻¹ for the switch to stationary adhesion and 0.042 s⁻¹ for the reversion from stationary to moving. When the flow rate is switched from low to high, the fluid movement was observed to increase in speed in less than one frame (37 ms), but the switch from high to low took place over several seconds, probably due to a slow decrease in pressure in the tubing between pump and chamber. This may explain why the response is a little slow at first for this transition.

FIGURE 7

Alternative models. (A) Two-pathway bond model. (B) Two independent binding sites model. In each model, each rate constant reflects an unstressed rate constant and a transition state distance

FIGURE 8

Tests of alternative models. (A) The two-pathway model (16) (dotted line) does not describe a typical FimH data set (green diamonds; 0.01 pN/μm²) because the model requires single exponential decay. The two independent binding sites model (solid lines) requires that the high shear data (red squares; 2 pN/μm²) be shifted downward by assuming a large number of bonds broke too quickly to cause observable pauses. The resulting large number of estimated bonds can be seen as the red square outliers in panel B. (B) When the two independent binding sites model was fit to the entire data set, the total number of estimated bonds served as a poor predictor of distance rolled, unlike for the allosteric catch-bond model in Fig. 5 B.