Superspreading and the effect of individual variation on disease emergence

Abstract

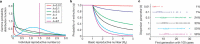
Population-level analyses often use average quantities to describe heterogeneous systems, particularly when variation does not arise from identifiable groups. A prominent example, central to our current understanding of epidemic spread, is the basic reproductive number, R(0), which is defined as the mean number of infections caused by an infected individual in a susceptible population. Population estimates of R(0) can obscure considerable individual variation in infectiousness, as highlighted during the global emergence of severe acute respiratory syndrome (SARS) by numerous 'superspreading events' in which certain individuals infected unusually large numbers of secondary cases. For diseases transmitted by non-sexual direct contacts, such as SARS or smallpox, individual variation is difficult to measure empirically, and thus its importance for outbreak dynamics has been unclear. Here we present an integrated theoretical and statistical analysis of the influence of individual variation in infectiousness on disease emergence. Using contact tracing data from eight directly transmitted diseases, we show that the distribution of individual infectiousness around R(0) is often highly skewed. Model predictions accounting for this variation differ sharply from average-based approaches, with disease extinction more likely and outbreaks rarer but more explosive. Using these models, we explore implications for outbreak control, showing that individual-specific control measures outperform population-wide measures. Moreover, the dramatic improvements achieved through targeted control policies emphasize the need to identify predictive correlates of higher infectiousness. Our findings indicate that superspreading is a normal feature of disease spread, and to frame ongoing discussion we propose a rigorous definition for superspreading events and a method to predict their frequency.

Figure 1. Evidence for variation in individual reproductive number ν.

a, Transmission data from the SARS outbreak in Singapore in 2003 (ref. 5). Bars show observed frequency of Z, the number of individuals infected by each case. Lines show maximum-likelihood fits for Z∼Poisson (squares), Z∼geometric (triangles), and Z∼negative binomial (circles). Inset, probability density function (solid) and cumulative distribution function (dashed) for gamma-distributed ν (corresponding to Z∼negative binomial) estimated from Singapore SARS data. b, Expected proportion of all transmission due to a given proportion of infectious cases, where cases are ranked by infectiousness. For a homogeneous population (all ν = R₀), this relation is linear. For five directly transmitted infections (based on k̂ values in Supplementary Table 1), the line is concave owing to variation in ν. c, Proportion of transmission expected from the most infectious 20% of cases, for 10 outbreak or surveillance data sets (triangles). Dashed lines show proportions expected under the 20/80 rule (top) and homogeneity (bottom). Superscript ‘v’ indicates a partially vaccinated population. d, Reported superspreading events (SSEs; diamonds) relative to estimated reproductive number R (squares) for twelve directly transmitted infections. Lines show 5–95 percentile range of Z∼Poisson(R), and crosses show the 99th-percentile proposed as threshold for SSEs. Stars represent SSEs caused by more than one source case. ‘Other’ diseases are: 1, Streptococcus group A; 2, Lassa fever; 3, Mycoplasma pneumonia; 4, pneumonic plague; 5, tuberculosis. R is not shown for ‘other’ diseases, and is off-scale for monkeypox. See Supplementary Notes for details.

Figure 2. Outbreak dynamics with different degrees of individual variation in infectiousness.

a, The individual reproductive number ν is drawn from a gamma distribution with mean R₀ and dispersion parameter k. Probability density functions are shown for six gamma distributions with R₀ = 1.5 (‘k = Inf’ indicates k → ∞). b, Probability of stochastic extinction of an outbreak, q, versus population-average reproductive number, R₀, following introduction of a single infected individual. The value of k increases from top to bottom (values and colours as in a). c, Growth of simulated outbreaks with R₀ = 1.5 and one initial case, conditional on non-extinction. Boxes show median and interquartile range (IQR) of the first disease generation with 100 cases; whiskers show most extreme values within 1.5 × IQR of the boxes, and crosses show outliers. Percentages show the proportion of 10,000 simulated outbreaks that reached the 100-case threshold (roughly 1 - q).

Figure 3. Implications for control measures.

a, Increase in extinction probability (q^ind - q^pop) under individual-specific control compared to population-wide control, for diseases with R₀ = 3 and different degrees of individual variation, k, subject to control effort c. With population-wide control, the infectiousness of all individuals is reduced by a factor c. With individual-specific control, a proportion c of infectious individuals (selected at random) have their infectiousness reduced to zero. The outbreak is assumed to begin with one case, with control present from the outset. b, Estimates of R̂ and k̂ from outbreak data sets before and after control measures were initiated (joined by solid lines; Supplementary Table 2), and post-control values of k_c estimated from theoretical models of control as described in the Supplementary Notes. c, Effect of random versus targeted control measures. The probability of outbreak containment (defined as never reaching the 100-case threshold) for four diseases with R₀ = 3 and k = 0.1 (blue), k = 0.5 (green), k = 1 (black) or k → ∞ (purple). Control policies are population-wide (solid lines), random individual-specific (dotted lines), or targeted individual-specific (dashed lines, where half of all control effort is focused on the most infectious 20% of cases). For k → ∞, all individuals are identical, so targeting has no effect and dotted and dashed lines overlay one another. d, The factor by which targeting increases the effect of control on preventing a major outbreak, relative to random individual-specific control (see Supplementary Notes), when 20%, 40% or 60% of the total population is controlled. Results in c and d are the mean of 10,000 simulations, with control beginning in the second generation of cases.