Predicting human chronically paralyzed muscle force: a comparison of three mathematical models
- PMID: 16306255
- PMCID: PMC3274555
- DOI: 10.1152/japplphysiol.00935.2005
Predicting human chronically paralyzed muscle force: a comparison of three mathematical models
Abstract
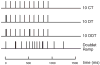
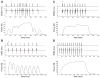
Chronic spinal cord injury (SCI) induces detrimental musculoskeletal adaptations that adversely affect health status, ranging from muscle paralysis and skin ulcerations to osteoporosis. SCI rehabilitative efforts may increasingly focus on preserving the integrity of paralyzed extremities to maximize health quality using electrical stimulation for isometric training and/or functional activities. Subject-specific mathematical muscle models could prove valuable for predicting the forces necessary to achieve therapeutic loading conditions in individuals with paralyzed limbs. Although numerous muscle models are available, three modeling approaches were chosen that can accommodate a variety of stimulation input patterns. To our knowledge, no direct comparisons between models using paralyzed muscle have been reported. The three models include 1) a simple second-order linear model with three parameters and 2) two six-parameter nonlinear models (a second-order nonlinear model and a Hill-derived nonlinear model). Soleus muscle forces from four individuals with complete, chronic SCI were used to optimize each model's parameters (using an increasing and decreasing frequency ramp) and to assess the models' predictive accuracies for constant and variable (doublet) stimulation trains at 5, 10, and 20 Hz in each individual. Despite the large differences in modeling approaches, the mean predicted force errors differed only moderately (8-15% error; P=0.0042), suggesting physiological force can be adequately represented by multiple mathematical constructs. The two nonlinear models predicted specific force characteristics better than the linear model in nearly all stimulation conditions, with minimal differences between the two nonlinear models. Either nonlinear mathematical model can provide reasonable force estimates; individual application needs may dictate the preferred modeling strategy.
Figures
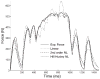

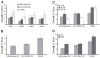



References
-
- Aaron SL, Stein RB. Comparison of an EMG-controlled prosthesis and the normal human biceps brachii muscle. Am J Phys Med. 1976;55:1–14. - PubMed
-
- Baratta RV, Zhou BH, Solomonow M. Frequency response model of skeletal muscle: effect of perturbation level, and control strategy. Med Biol Eng Comput. 1989;27:337–345. - PubMed
-
- Bawa P, Stein RB. Frequency response of human soleus muscle. J Neurophysiol. 1976;39:788–793. - PubMed
-
- Bobet J. Can muscle models improve FES-assisted walking after spinal cord injury? J Electromyogr Kinesiol. 1998;8:125–132. - PubMed
-
- Bobet J, Stein RB. A simple model of force generation by skeletal muscle during dynamic isometric contractions. IEEE Trans Biomed Eng. 1998;45:1010–1016. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

