Heat capacity changes associated with DNA duplex formation: salt- and sequence-dependent effects
- PMID: 16401089
- PMCID: PMC2465463
- DOI: 10.1021/bi0517178
Heat capacity changes associated with DNA duplex formation: salt- and sequence-dependent effects
Abstract
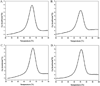
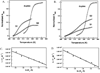
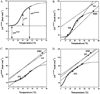
Duplexes are the most fundamental elements of nucleic acid folding. Although it has become increasingly clear that duplex formation can be associated with a significant change in heat capacity (deltaC(p)), this parameter is typically overlooked in thermodynamic studies of nucleic acid folding. Analogy to protein folding suggests that base stacking events coupled to duplex formation should give rise to a deltaC(p) due to the release of waters solvating aromatic surfaces of nucleotide bases. In previous work, we showed that the deltaC(p) observed by isothermal titration calorimetry (ITC) for RNA duplex formation depended on salt and sequence [Takach, J. C., Mikulecky, P. J., and Feig, A. L. (2004) J. Am. Chem. Soc. 126, 6530-6531]. In the present work, we apply calorimetric and spectroscopic techniques to a series of designed DNA duplexes to demonstrate that both the salt dependence and sequence dependence of deltaC(p)s observed by ITC reflect perturbations to the same fundamental phenomenon: stacking in the single-stranded state. By measuring the thermodynamics of single strand melting, one can accurately predict the deltaC(p)s observed for duplex formation by ITC at high and low ionic strength. We discuss our results in light of the larger issue of contributions to deltaC(p) from coupled equilibria and conclude that observed deltaC(p)s can be useful indicators of intermediate states in nucleic acid folding phenomena.
Figures
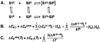




Similar articles
-
Enthalpy and heat capacity changes for formation of an oligomeric DNA duplex: interpretation in terms of coupled processes of formation and association of single-stranded helices.Biochemistry. 1999 Jun 29;38(26):8409-22. doi: 10.1021/bi990043w. Biochemistry. 1999. PMID: 10387087
-
The contribution of DNA single-stranded order to the thermodynamics of duplex formation.Proc Natl Acad Sci U S A. 1991 May 1;88(9):3569-73. doi: 10.1073/pnas.88.9.3569. Proc Natl Acad Sci U S A. 1991. PMID: 2023903 Free PMC article.
-
A thermodynamic study on the formation and stability of DNA duplex at transcription site for DNA binding proteins GCN4.Biophys Chem. 1999 Aug 30;80(3):217-26. doi: 10.1016/s0301-4622(99)00084-8. Biophys Chem. 1999. PMID: 10483711
-
Stabilities of double- and triple-strand helical nucleic acids.Prog Biophys Mol Biol. 1992;58(3):225-57. doi: 10.1016/0079-6107(92)90007-s. Prog Biophys Mol Biol. 1992. PMID: 1380719 Review.
-
Effects of 3,N4-ethenodeoxycytidine on duplex stability and energetics.IARC Sci Publ. 1999;(150):169-77. IARC Sci Publ. 1999. PMID: 10626218 Review.
Cited by
-
Linking Temperature, Cation Concentration and Water Activity for the B to Z Conformational Transition in DNA.Molecules. 2018 Jul 21;23(7):1806. doi: 10.3390/molecules23071806. Molecules. 2018. PMID: 30037061 Free PMC article.
-
Thermodynamic insights into 2-thiouridine-enhanced RNA hybridization.Nucleic Acids Res. 2015 Sep 18;43(16):7675-87. doi: 10.1093/nar/gkv761. Epub 2015 Aug 3. Nucleic Acids Res. 2015. PMID: 26240387 Free PMC article.
-
Thermodynamic and kinetic analysis of an RNA kissing interaction and its resolution into an extended duplex.Biophys J. 2012 Mar 7;102(5):1097-107. doi: 10.1016/j.bpj.2011.12.052. Epub 2012 Mar 6. Biophys J. 2012. PMID: 22404932 Free PMC article.
-
Thermodynamics of ligand binding to a heterogeneous RNA population in the malachite green aptamer.Biochemistry. 2012 Jan 10;51(1):565-72. doi: 10.1021/bi201642p. Epub 2011 Dec 16. Biochemistry. 2012. PMID: 22192051 Free PMC article.
-
Understanding the Contributions of Conformational Changes, Thermodynamics, and Kinetics of RNA-Small Molecule Interactions.ACS Chem Biol. 2019 May 17;14(5):824-838. doi: 10.1021/acschembio.8b00945. Epub 2019 May 1. ACS Chem Biol. 2019. PMID: 31042354 Free PMC article. Review.
References
-
- Cooper A. Heat capacity of hydrogen-bonded networks: an alternative view of protein folding thermodynamics. Biophys. Chem. 2000;85:25–39. - PubMed
-
- Cooper A, Johnson CM, Lakey JH, Nollmann M. Heat does not come in different colours: entropy-enthalpy compensation, free energy windows, quantum confinement, pressure perturbation calorimetry, solvation and the multiple causes of heat capacity effects in biomolecular interactions. Biophys. Chem. 2001;93:215–230. - PubMed
-
- Makhatadze GI. Heat capacities of amino acids, peptides and proteins. Biophys. Chem. 1998;71:133–156. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

