Optimal surface segmentation in volumetric images--a graph-theoretic approach
- PMID: 16402624
- PMCID: PMC2646122
- DOI: 10.1109/TPAMI.2006.19
Optimal surface segmentation in volumetric images--a graph-theoretic approach
Abstract
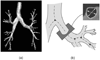
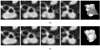
Efficient segmentation of globally optimal surfaces representing object boundaries in volumetric data sets is important and challenging in many medical image analysis applications. We have developed an optimal surface detection method capable of simultaneously detecting multiple interacting surfaces, in which the optimality is controlled by the cost functions designed for individual surfaces and by several geometric constraints defining the surface smoothness and interrelations. The method solves the surface segmentation problem by transforming it into computing a minimum s-t cut in a derived arc-weighted directed graph. The proposed algorithm has a low-order polynomial time complexity and is computationally efficient. It has been extensively validated on more than 300 computer-synthetic volumetric images, 72 CT-scanned data sets of different-sized plexiglas tubes, and tens of medical images spanning various imaging modalities. In all cases, the approach yielded highly accurate results. Our approach can be readily extended to higher-dimensional image segmentation.
Figures











References
-
- Montanari U. On the Optimal Detection of Curves in Noisy Pictures. Comm. ACM. 1971 May;vol. 14:335–345.
-
- Martelli A. Edge Detection Using Heuristic Search Methods. Computer Graphics and Image Processing. 1972 Aug.vol. 1:169–182.
-
- Martelli A. An Application of Heuristic Search Methods to Edge and Contour Detection. Comm. ACM. 1976 Feb.vol. 19:73–83.
-
- Pope D, Parker D, Clayton P, Gustafson D. Left Ventricular Border Detection Using a Dynamic Search. Radiology. 1985 May;vol. 155:513–518. - PubMed
-
- Schenk A, Prause G, Peitgen H-O. Local Cost Computation for Efficient Segmentation of 3D Objects with Live Wire; Proc. SPIE Int’l Symp. Medical Imaging: Image Processing; 2001. pp. 1357–1364.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

