Multiple events on single molecules: unbiased estimation in single-molecule biophysics
- PMID: 16439482
- PMCID: PMC1413656
- DOI: 10.1073/pnas.0510509103
Multiple events on single molecules: unbiased estimation in single-molecule biophysics
Abstract
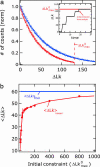
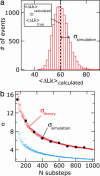
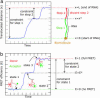
Most analyses of single-molecule experiments consist of binning experimental outcomes into a histogram and finding the parameters that optimize the fit of this histogram to a given data model. Here we show that such an approach can introduce biases in the estimation of the parameters, thus great care must be taken in the estimation of model parameters from the experimental data. The bias can be particularly large when the observations themselves are not statistically independent and are subjected to global constraints, as, for example, when the iterated steps of a motor protein acting on a single molecule must not exceed the total molecule length. We have developed a maximum-likelihood analysis, respecting the experimental constraints, which allows for a robust and unbiased estimation of the parameters, even when the bias well exceeds 100%. We demonstrate the potential of the method for a number of single-molecule experiments, focusing on the removal of DNA supercoils by topoisomerase IB, and validate the method by numerical simulation of the experiment.
Conflict of interest statement
Conflict of interest statement: No conflicts declared.
Figures
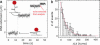
References
-
- Strick T. R.,, Croquette V., Bensimon D. Nature. 2000;404:901–904. - PubMed
-
- Visscher K., Schnitzer M. J., Block S. M. Nature. 1999;400:184–189. - PubMed
-
- Yildiz A., Forkey J. N., McKinney S. A., Ha T., Goldman Y. E., Selvin P. R. Science. 2003;300:2061–2065. - PubMed
-
- Weiss S. Science. 1999;283:1676–1683. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

