Prestressed F-actin networks cross-linked by hinged filamins replicate mechanical properties of cells
- PMID: 16446458
- PMCID: PMC1413620
- DOI: 10.1073/pnas.0504777103
Prestressed F-actin networks cross-linked by hinged filamins replicate mechanical properties of cells
Abstract
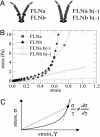
We show that actin filaments, shortened to physiological lengths by gelsolin and cross-linked with recombinant human filamins (FLNs), exhibit dynamic elastic properties similar to those reported for live cells. To achieve elasticity values of comparable magnitude to those of cells, the in vitro network must be subjected to external prestress, which directly controls network elasticity. A molecular requirement for the strain-related behavior at physiological conditions is a flexible hinge found in FLNa and some FLNb molecules. Basic physical properties of the in vitro filamin-F-actin network replicate the essential mechanical properties of living cells. This physical behavior could accommodate passive deformation and internal organelle trafficking at low strains yet resist externally or internally generated high shear forces.
Conflict of interest statement
Conflict of interest statement: No conflicts declared.
Figures


Similar articles
-
Cross-linking molecules modify composite actin networks independently.Phys Rev Lett. 2008 Sep 12;101(11):118102. doi: 10.1103/PhysRevLett.101.118102. Epub 2008 Sep 10. Phys Rev Lett. 2008. PMID: 18851335
-
Thermodynamics of filamin-actin interaction.Biochem Soc Trans. 1992 May;20(2):89S. doi: 10.1042/bst020089s. Biochem Soc Trans. 1992. PMID: 1397655 No abstract available.
-
Viscoelasticity of actin-gelsolin networks in the presence of filamin.Eur J Biochem. 1997 Jun 1;246(2):373-9. doi: 10.1111/j.1432-1033.1997.00373.x. Eur J Biochem. 1997. PMID: 9208927
-
Mechanical response of single filamin A (ABP-280) molecules and its role in the actin cytoskeleton.J Muscle Res Cell Motil. 2002;23(5-6):525-34. doi: 10.1023/a:1023418725001. J Muscle Res Cell Motil. 2002. PMID: 12785102 Review.
-
Structural portrait of filamin interaction mechanisms.Curr Protein Pept Sci. 2010 Nov;11(7):639-50. doi: 10.2174/138920310794109111. Curr Protein Pept Sci. 2010. PMID: 20887254 Review.
Cited by
-
Forcing cells into shape: the mechanics of actomyosin contractility.Nat Rev Mol Cell Biol. 2015 Aug;16(8):486-98. doi: 10.1038/nrm4012. Epub 2015 Jul 1. Nat Rev Mol Cell Biol. 2015. PMID: 26130009 Free PMC article. Review.
-
Mammary gland ECM remodeling, stiffness, and mechanosignaling in normal development and tumor progression.Cold Spring Harb Perspect Biol. 2011 Jan 1;3(1):a003228. doi: 10.1101/cshperspect.a003228. Cold Spring Harb Perspect Biol. 2011. PMID: 20980442 Free PMC article. Review.
-
Comparative analysis of the two extremes of FLNB-mutated autosomal dominant disease spectrum: from clinical phenotypes to cellular and molecular findings.Am J Transl Res. 2018 May 15;10(5):1400-1412. eCollection 2018. Am J Transl Res. 2018. PMID: 29887954 Free PMC article.
-
Cell response to substrate rigidity is regulated by active and passive cytoskeletal stress.Proc Natl Acad Sci U S A. 2020 Jun 9;117(23):12817-12825. doi: 10.1073/pnas.1917555117. Epub 2020 May 22. Proc Natl Acad Sci U S A. 2020. PMID: 32444491 Free PMC article.
-
Cell mechanics: principles, practices, and prospects.Wiley Interdiscip Rev Syst Biol Med. 2014 Sep-Oct;6(5):371-88. doi: 10.1002/wsbm.1275. Wiley Interdiscip Rev Syst Biol Med. 2014. PMID: 25269160 Free PMC article. Review.
References
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials
Miscellaneous

