A methodology for the structural and functional analysis of signaling and regulatory networks
- PMID: 16464248
- PMCID: PMC1458363
- DOI: 10.1186/1471-2105-7-56
A methodology for the structural and functional analysis of signaling and regulatory networks
Abstract
Background: Structural analysis of cellular interaction networks contributes to a deeper understanding of network-wide interdependencies, causal relationships, and basic functional capabilities. While the structural analysis of metabolic networks is a well-established field, similar methodologies have been scarcely developed and applied to signaling and regulatory networks.
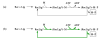
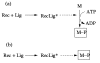
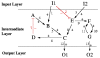
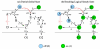
Results: We propose formalisms and methods, relying on adapted and partially newly introduced approaches, which facilitate a structural analysis of signaling and regulatory networks with focus on functional aspects. We use two different formalisms to represent and analyze interaction networks: interaction graphs and (logical) interaction hypergraphs. We show that, in interaction graphs, the determination of feedback cycles and of all the signaling paths between any pair of species is equivalent to the computation of elementary modes known from metabolic networks. Knowledge on the set of signaling paths and feedback loops facilitates the computation of intervention strategies and the classification of compounds into activators, inhibitors, ambivalent factors, and non-affecting factors with respect to a certain species. In some cases, qualitative effects induced by perturbations can be unambiguously predicted from the network scheme. Interaction graphs however, are not able to capture AND relationships which do frequently occur in interaction networks. The consequent logical concatenation of all the arcs pointing into a species leads to Boolean networks. For a Boolean representation of cellular interaction networks we propose a formalism based on logical (or signed) interaction hypergraphs, which facilitates in particular a logical steady state analysis (LSSA). LSSA enables studies on the logical processing of signals and the identification of optimal intervention points (targets) in cellular networks. LSSA also reveals network regions whose parametrization and initial states are crucial for the dynamic behavior. We have implemented these methods in our software tool CellNetAnalyzer (successor of FluxAnalyzer) and illustrate their applicability using a logical model of T-Cell receptor signaling providing non-intuitive results regarding feedback loops, essential elements, and (logical) signal processing upon different stimuli.
Conclusion: The methods and formalisms we propose herein are another step towards the comprehensive functional analysis of cellular interaction networks. Their potential, shown on a realistic T-cell signaling model, makes them a promising tool.
Figures
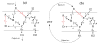


References
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

