Single Ih channels in pyramidal neuron dendrites: properties, distribution, and impact on action potential output
- PMID: 16467515
- PMCID: PMC6793638
- DOI: 10.1523/JNEUROSCI.3664-05.2006
Single Ih channels in pyramidal neuron dendrites: properties, distribution, and impact on action potential output
Abstract
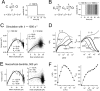
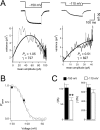
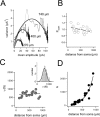
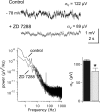
The hyperpolarization-activated cation current (Ih) plays an important role in regulating neuronal excitability, yet its native single-channel properties in the brain are essentially unknown. Here we use variance-mean analysis to study the properties of single Ih channels in the apical dendrites of cortical layer 5 pyramidal neurons in vitro. In these neurons, we find that Ih channels have an average unitary conductance of 680 +/- 30 fS (n = 18). Spectral analysis of simulated and native Ih channels showed that there is little or no channel flicker below 5 kHz. In contrast to the uniformly distributed single-channel conductance, Ih channel number increases exponentially with distance, reaching densities as high as approximately 550 channels/microm2 at distal dendritic sites. These high channel densities generate significant membrane voltage noise. By incorporating a stochastic model of Ih single-channel gating into a morphologically realistic model of a layer 5 neuron, we show that this channel noise is higher in distal dendritic compartments and increased threefold with a 10-fold increased single-channel conductance (6.8 pS) but constant Ih current density. In addition, we demonstrate that voltage fluctuations attributable to stochastic Ih channel gating impact on action potential output, with greater spike-timing precision in models with the experimentally determined single-channel conductance. These data suggest that, in the face of high current densities, the small single-channel conductance of Ih is critical for maintaining the fidelity of action potential output.
Figures

Similar articles
-
Hyperpolarization-activated current Ih disconnects somatic and dendritic spike initiation zones in layer V pyramidal neurons.J Neurophysiol. 2003 Oct;90(4):2428-37. doi: 10.1152/jn.00377.2003. Epub 2003 Jun 11. J Neurophysiol. 2003. PMID: 12801902
-
Dendritic hyperpolarization-activated currents modify the integrative properties of hippocampal CA1 pyramidal neurons.J Neurosci. 1998 Oct 1;18(19):7613-24. doi: 10.1523/JNEUROSCI.18-19-07613.1998. J Neurosci. 1998. PMID: 9742133 Free PMC article.
-
Calcium-activated potassium conductances contribute to action potential repolarization at the soma but not the dendrites of hippocampal CA1 pyramidal neurons.J Neurosci. 1999 Jul 1;19(13):5205-12. doi: 10.1523/JNEUROSCI.19-13-05205.1999. J Neurosci. 1999. PMID: 10377332 Free PMC article.
-
Control of Na+ spike backpropagation by intracellular signaling in the pyramidal neuron dendrites.Mol Neurobiol. 2000 Aug-Dec;22(1-3):129-41. doi: 10.1385/MN:22:1-3:129. Mol Neurobiol. 2000. PMID: 11414276 Review.
-
Plasticity of voltage-gated ion channels in pyramidal cell dendrites.Curr Opin Neurobiol. 2010 Aug;20(4):503-9. doi: 10.1016/j.conb.2010.06.006. Epub 2010 Aug 4. Curr Opin Neurobiol. 2010. PMID: 20691582 Review.
Cited by
-
Sparse bursts optimize information transmission in a multiplexed neural code.Proc Natl Acad Sci U S A. 2018 Jul 3;115(27):E6329-E6338. doi: 10.1073/pnas.1720995115. Epub 2018 Jun 22. Proc Natl Acad Sci U S A. 2018. PMID: 29934400 Free PMC article.
-
Corticospinal-specific HCN expression in mouse motor cortex: I(h)-dependent synaptic integration as a candidate microcircuit mechanism involved in motor control.J Neurophysiol. 2011 Nov;106(5):2216-31. doi: 10.1152/jn.00232.2011. Epub 2011 Jul 27. J Neurophysiol. 2011. PMID: 21795621 Free PMC article.
-
Protein kinase C activation mediates interferon-β-induced neuronal excitability changes in neocortical pyramidal neurons.J Neuroinflammation. 2014 Oct 29;11:185. doi: 10.1186/s12974-014-0185-4. J Neuroinflammation. 2014. PMID: 25359459 Free PMC article.
-
Self-organized and self-sustained ensemble activity patterns in simulation of mouse primary motor cortex.bioRxiv [Preprint]. 2025 Jan 14:2025.01.13.632866. doi: 10.1101/2025.01.13.632866. bioRxiv. 2025. PMID: 39868170 Free PMC article. Preprint.
-
The h channel mediates location dependence and plasticity of intrinsic phase response in rat hippocampal neurons.J Neurosci. 2008 May 28;28(22):5846-60. doi: 10.1523/JNEUROSCI.0835-08.2008. J Neurosci. 2008. PMID: 18509046 Free PMC article.
References
-
- Alvarez O, Gonzalez C, Latorre R (2002). Counting channels: a tutorial guide on ion channel fluctuation analysis. Adv Physiol Educ 26:327–341. - PubMed
-
- Berger T, Larkum ME, Luscher H-R (2001). High Ih channel density in the distal apical dendrite of layer V pyramidal cells increases bidirectional attenuation of EPSPs. J Neurophysiol 85:855–868. - PubMed
-
- Biel M, Schneider A, Wahl C (2002). Cardiac HCN channels: structure, function, and modulation. Trends Cardiovasc Med 12:206–212. - PubMed
-
- Brown HF, DiFrancesco D, Noble SJ (1979). How does adrenaline accelerate the heart? Nature 280:235–236. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Molecular Biology Databases
Miscellaneous
