Modelling in molecular biology: describing transcription regulatory networks at different scales
- PMID: 16524837
- PMCID: PMC1609346
- DOI: 10.1098/rstb.2005.1806
Modelling in molecular biology: describing transcription regulatory networks at different scales
Abstract
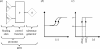
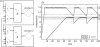
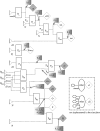
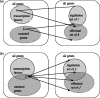
Approaches to describe gene regulation networks can be categorized by increasing detail, as network parts lists, network topology models, network control logic models or dynamic models. We discuss the current state of the art for each of these approaches. We study the relationship between different topology models, and give examples how they can be used to infer functional annotations for genes of unknown function. We introduce a new simple way of describing dynamic models called finite state linear model (FSLM). We discuss the gap between the parts list and topology models on one hand, and network logic and dynamic models, on the other hand. The first two classes of models have reached a genome-wide scale, while for the other model classes high-throughput technologies are yet to make a major impact.
Figures





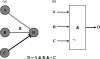
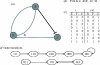
Republished in
-
Current approaches to gene regulatory network modelling.BMC Bioinformatics. 2007 Sep 27;8 Suppl 6(Suppl 6):S9. doi: 10.1186/1471-2105-8-S6-S9. BMC Bioinformatics. 2007. PMID: 17903290 Free PMC article.
References
-
- Akutsu T, Miyano S, Kuhara S. Identification of genetic networks from a small number of gene expression patterns under the Boolean network model. Pac. Symp. Biocomput. 1999:17–28. - PubMed
-
- Akutsu T, Miyano S, Kuhara S. Algorithms for inferring qualitative models of biological networks. Pac. Symp. Biocomput. 2000:293–304. - PubMed
-
- Ball P. Synthetic biology: starting from scratch. Nature. 2004;431:624–626. 10.1038/431624a - DOI - PubMed
-
- Becskei A, Serrano L. Engineering stability in gene networks by autoregulation. Nature. 2000;405:590–593. 10.1038/35014651 - DOI - PubMed
-
- Brazhnik P, de la Fuente A, Mendes P. Gene networks: how to put the function in genomics. Trends Biotechnol. 2002;20:467–472. 10.1016/S0167-7799(02)02053-X - DOI - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous
