The molecular elasticity of the insect flight muscle proteins projectin and kettin

Abstract

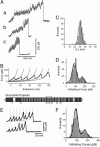
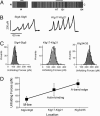
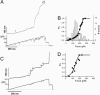
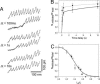
Projectin and kettin are titin-like proteins mainly responsible for the high passive stiffness of insect indirect flight muscles, which is needed to generate oscillatory work during flight. Here we report the mechanical properties of kettin and projectin by single-molecule force spectroscopy. Force-extension and force-clamp curves obtained from Lethocerus projectin and Drosophila recombinant projectin or kettin fragments revealed that fibronectin type III domains in projectin are mechanically weaker (unfolding force, F(u) approximately 50-150 pN) than Ig-domains (F(u) approximately 150-250 pN). Among Ig domains in Sls/kettin, the domains near the N terminus are less stable than those near the C terminus. Projectin domains refolded very fast [85% at 15 s(-1) (25 degrees C)] and even under high forces (15-30 pN). Temperature affected the unfolding forces with a Q(10) of 1.3, whereas the refolding speed had a Q(10) of 2-3, probably reflecting the cooperative nature of the folding mechanism. High bending rigidities of projectin and kettin indicated that straightening the proteins requires low forces. Our results suggest that titin-like proteins in indirect flight muscles could function according to a folding-based-spring mechanism.

Fig. 1.

Flexibility of single projectin molecules. (A) Rotary-shadowed EM showing individual projectin proteins (micrograph courtesy of Kevin Leonard, European Molecular Biology Laboratory, Heidelberg, Germany). The gray line shows the measured contour length, L_c, and the black line shows the measured end-to-end distance, x. (B) Plot of the square of the average x as a function of the contour length (filled circles) (data obtained from 20 molecules). The solid line is a nonlinear fit of Eq. 1, giving a value of P=30 nm. The dashed lines correspond to fits of P=20 and 40 nm.

Fig. 2.

Force–extension relationships of projectin molecules. (A) Several examples of force–extension curves obtained after stretching single projectin molecules. (B) To analyze the spacing between peaks in the sawtooth patterns we used the wormlike chain model. The lines were generated by using P=0.4 nm and ΔL_c=29 nm. (C) Histogram of contour length increments observed upon unfolding, ΔL_c (Gaussian fit: 30.1 ± 4.3 nm, n=362). (D) Histogram of force peaks shows two main peaks (Gaussian fits: 89.1 pN and 172.3 pN; mean force peak value: 109.4 ± 41 pN, n=479). (E) (Lower) Mechanical properties of a projectin recombinant fragment containing three Ig and four FnIII domains (PIg24–PIg26). (Upper) Domain structure of Drosophila projectin. (F) Histogram of unfolding forces for PIg24–PIg26 shows two peaks, one at ≈83 pN and the other at ≈171pN (n=142).

Fig. 3.

Force–extension relationships of recombinant kettin and N-terminal Sls fragments. (A) Location of the SIg4–SIg6, KIg17–KIg21, and KIg34/35 in the Sls/kettin sequence. The two blocks of sequence are spliced products of the Drosophila sls gene; the longer protein is kettin. (B) Examples of force–extension patterns obtained from the three-Ig (Left) and five-Ig (Right) fragment. (C) Histogram of unfolding forces for the proteins SIg4–SIg6, KIg17–KIg21, and KIg34/35 show that their mean unfolding forces are 123 ± 24 pN (n=371), 193 ± 52 pN (n=104), and 248 ± 34 pN (n=192), respectively. (D) Plot of the mean unfolding forces of SIg4–SIg6, KIg17–KIg21, and KIg34/35 proteins vs. their locations in the Sls and kettin sequence. Linear regression shows a slope of 4.4 pN per domain.

Fig. 4.

Measurements of the force dependence of the unfolding probability of projectin and kettin molecules. (A and C) Stepwise unfolding of single native projectin and a five-Ig kettin (KIg17–KIg21) fragment using the force-ramp method. The lower trace shows the time course of the force. (B) Frequency histogram of unfolding forces (bars) and the unfolding probability, P_u (filled squares) as a function of the applied force measured for six projectin molecules with similar number of unfolding events (86 total steps). The pulling speed was 200 pN/s. The lines correspond to the prediction of Eq. 5 using α₀₁=7 × 10⁻² s⁻¹ and Δx_u1=0.1 nm and α₀₂=0.3 × 10⁻³ s⁻¹ and Δx_u2=0.2 nm (continuous line). (D) Plot of the unfolding probability, P_u, as a function of the applied force for the KIg17–KIg21 kettin fragment (filled circles, 19 steps from 4 experiments). The pulling speed was 150 pN/s. The line corresponds to the prediction of Eq. 4 using α₀=9 × 10⁻³ s⁻¹ and Δx=0.17 nm.

Fig. 5.

Refolding kinetics of projectin domains. (A) The time interval between extensions affects the fraction of refolded domains (recorded at 13°C). (B) Fraction of refolded domains as a function of the time delay between stretching pulses, measured at 13°C (filled triangles) and 25°C (filled circles). The solid lines are a two-exponential fit of the data to the function N_refolded/N_total=A₁(1 − e^{−t·β 1}) + A₂(1 − e^{−Δt·β 2}), where A₁=0.7, A₂=0.3, β₁=6 s⁻¹, and β₂=0.1 s⁻¹ at 13°C, and A₁=0.85, A₂=0.15, β₁=15 s⁻¹, and β₂=0.18 s⁻¹ at 25°C. (C) Plot of the fraction of refolded domains, N_refolded/N_total, vs. the degree of relaxation, L₀/L_c, for two projectin molecules. The open triangles correspond to a Monte-Carlo simulation using an β₀=15 s⁻¹ and Δx_f=1.1 nm. The line is a polynomial fit to the Monte-Carlo simulation data.

Fig. 6.

Collapse of unfolded projectin domains under force. (A) Example of a projectin molecule that was first unfolded and extended at a high force (97 pN; the applied force is shown in the lower trace), then relaxed to a force of 15 pN and extended again at a force of 97 pN. (B) Example of a projectin molecule that was first unfolded and extended at 124 pN then relaxed to 30 pN and then to ≈5 pN (marked by arrowheads). After ≈5 s, the force was increased to 150 pN. (C) A projectin molecule was extended at a force of 115 pN then relaxed to 48 pN and, after 12 s, extended again at a force of 100 pN.