Channel density regulation of firing patterns in a cortical neuron model

Abstract

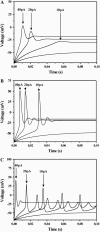
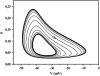
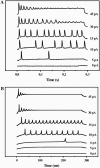
Modifying the density and distribution of ion channels in a neuron (by natural up- and downregulation or by pharmacological intervention or by spontaneous mutations) changes its activity pattern. In this investigation we analyzed how the impulse patterns are regulated by the density of voltage-gated channels in a neuron model based on voltage-clamp measurements of hippocampal interneurons. At least three distinct oscillatory patterns, associated with three distinct regions in the Na-K channel density plane, were found. A stability analysis showed that the different regions are characterized by saddle-node, double-orbit, and Hopf-bifurcation threshold dynamics, respectively. Single, strongly graded action potentials occur in an area outside the oscillatory regions, but less graded action potentials occur together with repetitive firing over a considerable range of channel densities. The relationship found here between channel densities and oscillatory behavior may partly explain the difference between the principal spiking patterns previously described for crab axons (class 1 and 2) and cortical neurons (regular firing and fast spiking).

FIGURE 1

Features of the neuron model. Computed action potentials at different channel densities, demonstrating density-dependent changes in gradedness and oscillatory behavior. The low density case (A), P*_Na = 1.3 × 10⁻⁶ and P*_K = 0.24 × 10⁻⁶ m s⁻¹, shows high sensitivity (graded amplitude), the high Na/low K channel density case (B), P*_Na = 30 × 10⁻⁶ and P*_K = 0.24 × 10⁻⁶ m s⁻¹, shows low sensitivity (all-or-nothing-like behavior) and the high density case (C), P*_Na = 26 × 10⁻⁶ and P*_K = 4.8 × 10⁻⁶ m s⁻¹, shows repetitive firing. Applied current was 5, 10, 20, and 40 pA.

FIGURE 2

Responses of the neuron model to increased stimulation current at different channel densities, demonstrating different onset (left) and termination (right) patterns of the oscillations. The high density case (A), with permeability values P*_Na = 20 × 10⁻⁶ and P*_K = 20 × 10⁻⁶ m s⁻¹, displays an abrupt onset and abrupt termination, case (B) with permeability values P*_Na = 20 × 10⁻⁶ and P*_K = 10 × 10⁻⁶ m s⁻¹, displays an abrupt onset and a continuous amplitude decrease at termination and case (C), with permeability values P*_Na = 20 × 10⁻⁶ and P*_K = 5 × 10⁻⁶ m s⁻¹, displays a continuous onset and a continuous amplitude decrease at termination.

FIGURE 3

Regions in the P*_Na-P*_K plane showing where the neuron model fires repetitively at the stimulation currents indicated.

FIGURE 4

Double-orbit bifurcation dynamics. Projection of a trajectory on the n-v plane of a region A2 neuron model stimulated by 18 pA. The trajectory starts at the inner unstable orbit and moves clockwise toward the outer stable orbit. Model permeability values are P*_Na = 14 × 10⁻⁶ and P*_K = 10 × 10⁻⁶ m s⁻¹.

FIGURE 5

Bifurcation map. Regions in the P*_Na-P*_K plane associated with oscillatory activity of double-orbit (A2), Hopf (B), and saddle-node (C1) bifurcation behavior of the neuron model at some stimulation interval. The oscillatory region is the envelope of all the oscillatory regions in Fig. 3.

FIGURE 6

Encoding functions for the model neuron. Oscillation frequency (A) and steady-state impulse amplitude (B) dependence on stimulation and channel densities (P*_Na/P*_K pairs). (C) The location of the illustrated cases in the P*_Na-P*_K plane, demonstrating that all oscillatory subregions are represented (see Fig. 5). The curves are denoted by associated P*_Na/P*_K values in the dimension of 10⁻⁶ m s⁻¹. Also indicated are the oscillatory subregions of the P*_Na/P*_K pairs.

FIGURE 7

Impulse amplitude-stimulus diagrams showing the amplitude sensitivity to stimulation of the model neuron. Changed K channel density and constant Na channel density (A), and changed Na channel densities and constant K channel density (B). (C) The location of the illustrated cases in the P*_Na-P*_K plane (see Fig. 5). The curves are denoted by associated P*_Na/P*_K values in the dimension of 10⁻⁶ m s⁻¹. Also indicated are the oscillatory subregions in the P*_Na-P*_K plane.

FIGURE 8

Pulse amplitude sensitivity to stimulation plotted in the channel density plane (P*_Na-P*_K). Sensitivity given as the range of stimulation current at which the current derivative of the impulse peak exceeds 0.25 mV pA⁻¹ as described in the text. The numbers marking the contours are range values in pA. High stimulus sensitivity, i.e., a strongly graded impulse, is reflected in a high range value. The dotted line indicates the oscillatory region, shown in Fig. 5. The circles denote the locations of the cases in Fig. 1; the strongly graded case to the left, the all-or-nothing-like case to the (lower) right, and the medium graded/repetitive firing case in between (upper right).

FIGURE 9

Saddle-node bifurcation behavior in a hippocampal interneuron. (A) Recordings from a mossy cell in the dentate gyrus with patch-clamp technique (whole-cell configuration). Stimulation current 5, 10, 20, 30 pA. Experimental details are given in (46). (B) Computed activity of the model neuron at channel densities P*_Na = 14 × 10⁻⁶ and P*_K = 2 × 10⁻⁶ m s⁻¹, located in region C1 (saddle-node bifurcation region) for stimulation currents 5, 10, and 15 pA.