Mechanism of beta4 subunit modulation of BK channels

Abstract

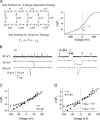
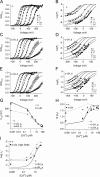
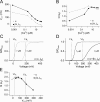
Large-conductance (BK-type) Ca(2+)-activated potassium channels are activated by membrane depolarization and cytoplasmic Ca(2+). BK channels are expressed in a broad variety of cells and have a corresponding diversity in properties. Underlying much of the functional diversity is a family of four tissue-specific accessory subunits (beta1-beta4). Biophysical characterization has shown that the beta4 subunit confers properties of the so-called "type II" BK channel isotypes seen in brain. These properties include slow gating kinetics and resistance to iberiotoxin and charybdotoxin blockade. In addition, the beta4 subunit reduces the apparent voltage sensitivity of channel activation and has complex effects on apparent Ca(2+) sensitivity. Specifically, channel activity at low Ca(2+) is inhibited, while at high Ca(2+), activity is enhanced. The goal of this study is to understand the mechanism underlying beta4 subunit action in the context of a dual allosteric model for BK channel gating. We observed that beta4's most profound effect is a decrease in P(o) (at least 11-fold) in the absence of calcium binding and voltage sensor activation. However, beta4 promotes channel opening by increasing voltage dependence of P(o)-V relations at negative membrane potentials. In the context of the dual allosteric model for BK channels, we find these properties are explained by distinct and opposing actions of beta4 on BK channels. beta4 reduces channel opening by decreasing the intrinsic gating equilibrium (L(0)), and decreasing the allosteric coupling between calcium binding and voltage sensor activation (E). However, beta4 has a compensatory effect on channel opening following depolarization by shifting open channel voltage sensor activation (Vh(o)) to more negative membrane potentials. The consequence is that beta4 causes a net positive shift of the G-V relationship (relative to alpha subunit alone) at low calcium. At higher calcium, the contribution by Vh(o) and an increase in allosteric coupling to Ca(2+) binding (C) promotes a negative G-V shift of alpha+beta4 channels as compared to alpha subunits alone. This manner of modulation predicts that type II BK channels are downregulated by beta4 at resting voltages through effects on L(0). However, beta4 confers a compensatory effect on voltage sensor activation that increases channel opening during depolarization.

Figure 1.

The effects of β4 on the mslo steady-state G-V relation vary with [Ca²⁺]. (A) Examples of currents evoked by voltage steps in 7 μM [Ca²⁺]. α alone is shown in the left panel, α+β4 is shown in the right panel. (B) Mean G-V relations at different [Ca²⁺] for α alone and α+β4. Each point represents mean data from 8 to 44 experiments. Solid curves represent fits to the Boltzmann function. (C) Mean V_1/2 values plotted as a function of [Ca²⁺]. β4 shifts V_1/2 toward more positive voltages <18.5 μM [Ca²⁺], and toward more negative voltages >18.5 μM [Ca²⁺]. Inset, α+β4 V_1/2 subtracted from mean α alone values. (D) Mean effective gating charge, Q, plotted as a function of [Ca²⁺]. In the presence of β4 there is a decrease in Q, and a more dramatic increase in Q can be observed as [Ca²⁺] increases. (E) Mean P_o as a function of voltage in the absence (5–7 patches) and presence (2–6 patches) of β4 in 300 nM Ca²⁺. Error bars represent SEM.

Figure 2.

Ability of 10 mM Mg²⁺ to promote channel gating is decreased in the presence of β4. (A) BK α (top) and α+β4 (bottom) currents are recorded in 60 μM Ca²⁺/0 Mg²⁺ (left) and 60 μM Ca²⁺/10 mM Mg²⁺ (right). (B) Conductance–voltage relationships in 60 μM Ca²⁺ with (5 patches for α and 9 patches α+β4) and without 10 mM MgCl₂ (9 patches for α and 17 patches α+β4) or (C) nominally 0 Ca²⁺ with (7 patches for α and 6 patches α+β4) and without (12 patches for α and 6 patches α+β4) 10 mM MgCl₂. Error bars represent SEM.

(SCHEME 1)

Figure 3.

β4 increases the intrinsic energetic barrier for channel to open. (A, left) According to the dual-allosteric mechanism (Horrigan and Aldrich, 1999, 2002), BK channel transitions between closed (C) and open (O) conformation is allosterically regulated by the state of four independent and identical voltage sensors. Sub-Scheme 1a represents BK channel's gating scheme at 0 Ca²⁺. Channel resides in either open or closed conformation, with 0–4 voltage sensors in the activated state. Equilibrium between C-O transitions is allosterically regulated by the states of the voltage sensors. Sub-Scheme 1b represents BK channel's gating scheme at 0 Ca²⁺ and very negative voltages. With all voltage sensors in the resting state, channel resides in one of two conformations, C₀ and O₀. Equilibrium between the C₀–O₀ transition is described by L, the intrinsic equilibrium for channel opening in the absence of Ca²⁺ and voltage sensor activation. (A, right) Illustration of how two components of L (L₀ and z_L) can be estimated by logPo-V data at 0 Ca²⁺ and negative voltages. Curve represents simulated logPo vs. voltage curve in nominally 0 Ca²⁺. Gating parameters used for simulation are as follows; L₀ = 2.5 × 10⁻⁶, z_L = 0.39 e₀, z_J = 0.54 e₀, Vh_c = 173 mV, Vh_o = 25 mV. Dashed line represents fit for logPo-V at limiting slope using Eq. 4. L₀ and z_L can be derived from the fit. (B) Single-channel BK currents recorded in nominally 0 Ca²⁺ at indicated voltages. At −80 mV, α alone data was obtained from a patch containing ∼706 channels, and α+β4 data was obtained from a patch containing estimated ∼730 channels. At both −40 and +40 mV, α alone data was obtained from a patch with estimated ∼123 channels, and α+β4 data was obtained from a patch with estimated ∼411 channels. All traces were low-pass filtered at 3 kHz, except for α alone at −80 mV, which was filtered at 8.4 kHz. (C) Limiting slope is not reached for the logP_o-V data in the presence of β4. Mean logP_o as a function of voltage in the absence and presence of β4 in nominally 0 Ca²⁺ (3–12 patches for α and 4–11 patches for α+β4). Error bars represent SEM. The voltage dependence (slope) for α alone channels shows an apparent decrease at approximately +30 mV. For α+β4 channels, no apparent change in slope is observed over the voltage range between −80 and +70 mV. (D) β4 decreases L₀ by at least 11-fold. Data from C replotted to show that estimates of L₀ for α alone channels obtained by extrapolating logP_o-V relations from limiting slope to 0 mV. An upper limit of L₀ for α+β4 channels was estimated using Eq. 4, based on the mean P_o value at −80 mV and a z_L value of 0.3 e₀.

Figure 4.

β4 effects on z_L in the presence of Ca²⁺. (A, left) According to the dual-allosteric mechanism (Horrigan and Aldrich, 2002), BK channel transitions between closed (C) and open (O) conformation is allosterically regulated by the state of four independent and identical Ca²⁺ binding sites. Sub-Scheme 1c represents BK channel's gating scheme at very negative voltages, where voltage sensors remain in the resting states. Channel resides in either closed or open conformations, with 0–4 Ca²⁺ binding sites occupied. Equilibrium between the C–O transitions is allosterically regulated by the states of the Ca²⁺ binding sites. In the absence of voltage sensor activation, voltage dependence of the C–O transition is entirely dependent on z_L. (A, right) Illustration of how z_L can be estimated by logP_o-V data at high Ca²⁺ and very negative voltages. Curves are simulated logP_o-V curves in nominally 0 Ca²⁺ and 100 μM Ca²⁺ according to Scheme 1c. Gating parameters used for simulation are as follows: L₀ = 2.5 × 10⁻⁶, z_L = 0.39 e₀, z_J = 0.54 e₀, Vh_c = 173 mV, Vh_o = 25 mV, K_c = 13.9 μM, and K_o = 1.4 μM. Dashed lines represent fits for logP_o-V at limiting slopes using Eq. 8. L₀′ and z_L can be derived from the fits. (B) At 100 μM Ca²⁺, currents were recorded at very negative voltages to determine logP_o vs. V relations. Currents were low-pass filtered at 20 kHz. Representative current traces at indicated voltages in the absence and presence of β4, respectively. Traces in B were all obtained from the same patch. Currents were filtered at 5 kHz for display purposes. (C) Representative logP_o-V relations at various Ca²⁺ where limiting slopes is reached. Upper limits for z_L were estimated from the apparent limiting slopes (solid lines). (D) Estimates of z_L plotted as a function of [Ca²⁺] for α subunits alone (open symbols) and α+β4 (closed symbols) for patches where limiting slope was reached. Error bars represent SEM. The number of patches where limiting slope was reached as well as total number of recordings performed (in parenthesis) at each [Ca²⁺] are indicated.

Figure 5.

Effect of β4 on Ca²⁺-dependent gating. (A) Symbols represent logP_o-V relations at various [Ca²⁺]. Error bars represent SEM. Lines are fits for mean logP_o-V at limiting slope using Eq. 8 and z_L of 0.3 e₀. L₀′ for α alone channels were derived from the fits. (B) Open symbols are logL₀′ vs. [Ca²⁺] for α alone. Curve represents fit of logL₀′-[Ca²⁺] using Eq. 7. For α+β4, only an upper limit for logL₀′ is estimated and displayed as solid symbols (solid circles with an overhanging line) and therefore were not fit with Eq. 7.

Figure 6.

Evaluation of fit parameters α, α+β4_a, and α+β4_b. P_o-V relations at 0.0005, 0.3, 1.7, 7, 18.5 and 100 μM Ca²⁺ were simulated using indicated fit parameters (Table III) and fit to the Boltzmann function. (A and B) The fit from α is superimposed on a series of G-V data for α alone channels from macroscopic recordings, and P_o-V data from single channel recordings, respectively. (C and D) The fit from α+β4_a (fit to G-V and low voltage P_o-V relations) is superimposed on G-V and P_o-V data for α+β4 channels, respectively. (E and F) The fit from α+β4_b (fit to G-V only) is superimposed on the same series of data as in C and D. (G) V_1/2 vs. [Ca²⁺], (H) Q vs. [Ca²⁺], and (I) logL₀′ vs. [Ca²⁺]. Simulations based on fit parameters (Table III) are compared with mean ± SEM of measurements (symbols).

Figure 7.

Evaluation of fit parameters α+β4_c through α+β4_f. Fits are superimposed on the same series of G-V (left) and P_o-V data (right). Individual parameters that are fixed are shown on the right. Parameters obtained are shown in Table III. (A) Best fit (α+β4_a) from Fig. 6 (C and D) for comparison. Fixed parameters are (B) increasing L₀ threefold to 1.8 e⁻⁷, (C) decreasing L₀ threefold to 1.2 e⁻⁸, (D) 50 mV positive shift of Vh_o to 0 mV, (E) −50 mV shift of Vh_o to −100 mV.

Figure 8.

Changes in G-V relations as a consequence of β4 modulation of L₀. Simulations using α subunit parameters from Table III, with α L₀ (plus symbols) or α+β4 L₀ (closed symbols). (A) Effect of L₀ modulation on V_1/2 vs. [Ca²⁺] relationship, and (B) Q vs. [Ca²⁺] relationship. V_1/2 and Q of simulated G-V were obtained from Boltzmann fit to simulated P_o-V curves. (C–E) Illustration of how L₀ and [Ca²⁺] affect Q by influencing position of G-V curves relative to Vh_o and Vh_c. (C) Simulation of G-V curves in 7 μM (dashed line) and 0 calcium (solid line) relative to Vh_o and Vh_c (vertical dash lines) using α subunit L₀ parameter. (D) Same as C but using α+β4 L₀ parameter. (E) Q vs. V_1/2 relationships illustrates how position of V_1/2 relative to Vh_o and Vh_c affects Q values.

Figure 9.

Negative shift of Vh_o has the most significant contribution in opposing decrease in L₀ and increasing α+β4 channel opening. Data points are simulated values based on α subunit parameters in Table III with indicated parameters replaced by those of α+β4. (A and B) Effects of β4 modulation on Ca²⁺-dependent gating. (C and D) Changes in G-V relations as a consequence of β4 modulation on voltage-dependent gating. Plotted are V_1/2-[Ca²⁺] and Q-[Ca²⁺] relations when α parameters are replaced by indicated α+β4 parameters.

Figure 10.

Additive effects of β4 gating parameters on BK channel steady-state properties. Simulations with α subunit parameters incrementally replaced by those of α+β4. Panels show experimental data for α (open symbols) and α+β4 (closed symbols) V_1/2 vs. [Ca²⁺] relationship. Line shows simulations using α subunit parameters incrementally altered by β4 L₀ (A), β4 L₀ + D (B), β4 L₀ + D +C (C), β4 L₀ + D +C +E (D).