Turing instability mediated by voltage and calcium diffusion in paced cardiac cells

Abstract

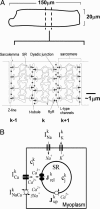
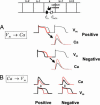
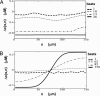
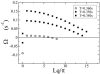
In cardiac cells, the coupling between the voltage across the cell membrane (V(m)) and the release of calcium (Ca) from intracellular stores is a crucial ingredient of heart function. Under abnormal conditions and/or rapid pacing, both the action potential duration and the peak Ca concentration in the cell can exhibit well known period-doubling oscillations referred to as "alternans," which have been linked to sudden cardiac death. Fast diffusion of V(m) keeps action potential duration alternans spatially synchronized over the approximately 150-mum-length scale of a cell, but slow diffusion of Ca ions allows Ca alternans within a cell to become spatially asynchronous, as observed in some experiments. This finding raises the question: When are Ca alternans spatially in-phase or out-of-phase on subcellular length scales? This question is investigated by using a spatially distributed model of Ca cycling coupled to V(m). Our main finding is the existence of a Turing-type symmetry breaking instability mediated by V(m) and Ca diffusion that causes Ca alternans to become spontaneously out-of-phase at opposite ends of a cardiac cell. Pattern formation is governed by the interplay of short-range activation of Ca alternans, because of a dynamical instability of Ca cycling, and long-range inhibition of Ca alternans by V(m) alternans through Ca-sensitive membrane ionic currents. These results provide a striking example of a Turing instability in a biological context where the morphogens can be clearly identified, as well as a potential link between dynamical instability on subcellular scales and life-threatening cardiac disorders.

Fig. 1.

Illustration of cardiac cell architecture and ionic model. (A) Schematic representation of the structure of the cardiac cell. The cell is divided into subcellular units, which correspond to sarcomeres. (B) Illustration of Ca cycling machinery along with ion currents that regulate V_m within a sarcomere.

Fig. 2.

Illustration of bidirectional coupling between Ca and V_m. (A) Coupling between the APD and the Ca transient on the next beat. (B) Coupling between the Ca transient and the APD on the same beat.

Fig. 3.

Spatiotemporal dynamics of subcellular Ca alternans in a cell with 75 sarcomeres for two different strengths of Ca-induced inactivation of the L-type Ca current. (A) Weak Ca-induced inactivation (positive Ca → V_m coupling) leads to spatial synchronization of alternans. The thick black line corresponds to the steady-state Ca alternans amplitude. The pacing rate is 0.35 s, with T_c = 0.37 s. (B) Strong Ca-induced inactivation (negative Ca → V_m coupling) leads to spontaneous symmetry breaking resulting in desynchronization of two halves of the cell. The pacing rate is 0.35 s, with T_c = 0.344 s. Detailed parameters of the ionic model are given in Tables 1–7, which are published as supporting information on the PNAS web site.

Fig. 4.

Numerically computed linear stability spectrum showing the exponential amplification rate Ω of sinusoidal perturbations of the spatially uniform steady state with no alternans vs. the dimensionless wavenumber qL/π for different pacing periods T = 0.34, 0.35, and 0.36 s. For all periods, the fastest-growing wavelength is twice the cell length (q = π/L). The model parameters are the same as those that yielded the asynchronous state in Fig. 3B.

Fig. 5.

Analogy to a Turing instability mechanism. (A) Ca alternans amplitude as short-range activator. The red line of the Ca trace corresponds to Ca alternans that have larger amplitude than that shown by the black line. The effect on the V_m trace is to increase the amplitude of APD alternans. (B) APD alternans amplitude as long-range inhibitor. An increase in APD alternans amplitude leads to a decrease in Ca alternans amplitude on the next beat.