Collegial decision making based on social amplification leads to optimal group formation

Abstract

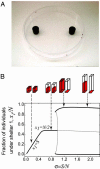
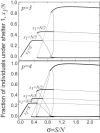
Group-living animals are often faced with choosing between one or more alternative resource sites. A central question in such collective decision making includes determining which individuals induce the decision and when. This experimental and theoretical study of shelter selection by cockroach groups demonstrates that choices can emerge through nonlinear interaction dynamics between equal individuals without perfect knowledge or leadership. We identify a simple mechanism whereby a decision is taken on the move with limited information and signaling and without comparison of available opportunities. This mechanism leads to optimal mean benefit for group individuals. Our model points to a generic self-organized collective decision-making process independent of animal species.

Fig. 1.

Experimental setup and bifurcation diagram of the collective choice predicted by the model. (A) Choice tests with groups of cockroaches were made in Petri dishes (14 cm) with small plastic caps for shelters. Numbers of individuals in each shelter were recorded during the resting period 24 h after the beginning of the test. (B) Steady states of Eqs. 3 and 4, giving the fraction of individuals in one shelter as a function of the ratio of the carrying capacity and total individual number σ with the measured values μ = 0.001 s⁻¹, θ = 0.01 s⁻¹, ρ = 1667, n = 2. The steady states and their stability are solved numerically with maple. Thick line, stable state; thin line, unstable state. Only one of the shelters is represented for symmetry reason. Above the graph, the corresponding shelter-filling outcome. When σ < 1, only one solution exists, corresponding to an equal number of individuals in each shelter. When σ < 1/2, the individuals fill the two shelters up to their maximum (x₁ = x₂ = S). When σ > 1/2, a plateau value is reached corresponding to equipartition of the individuals (x₁/N = x₂/N = 1/2). When σ > 1, three solutions exist, among which one is unstable and corresponds to equipartition, and the two stable states correspond to all individuals in one of the shelters i.e., [x₁ ≈ 0; x₂/N ≈ 1; x_e ≈ 0] or [x₁/N ≈ 1; x₂ ≈ 0; x_e ≈ 0].

Fig. 2.

Experimental individual distributions among shelters and bifurcation diagram. We report on 263 experiments for 10 combinations of N and S that were tested corresponding to 10 different values of the ratio σ. Three values of N and six values of S were used. Blue bars represent the experimental observed frequency of individual distributions for each σ value, related to the population fraction in shelter 1. Light blue bars correspond to the highest experimental frequencies. (A) White bars predicted steady-state distribution by stochastic simulations of the model. The four values of σ correspond to arrows in Fig. 1B. For σ = 0.5 and σ = 0.84, i.e., before the bifurcation point predicted in Fig. 1B, the observed distributions are equipartitioned between the two shelters i.e., the class 40–60%; meaning that half of the individuals are in shelter 1, which is the distribution predicted by the model. Because no individual remained outside, the other half was in the other shelter. The predicted plateau value of equipartition is observed experimentally. The possible solution of filling first one shelter and then the other shelter is not selected. Above the bifurcation, for σ = 1.25 and σ = 2.20, the most frequently observed distribution corresponds to all individuals selecting the same shelter. The highest observation frequencies are classes 0–20% or 80–100%, with equal observation frequency. This means that nearly all of the individuals were either in shelter 1 or in shelter 2 and that the choice between them is random. (B) Experimental bifurcation diagram, as a function of σ, in quantitative agreement with the model.

Fig. 3.

Bifurcation diagrams showing the fraction of individuals in one shelter, (x₁) in relation to σ with the measured values μ = 0.001 S⁻¹, θ = 0.01 S⁻¹, and ρ = 1667; n = 2. Panels show examples for p = 3 and p = 4 shelters; thin lines, unstable states; thick lines, stable states. For p = 3 and for low values of S, the only stable solution is equipartition of individuals among the three shelters (x₁ = x₂ = x₃). When S increases (S ≈ N/2), this state becomes unstable. The stable branch corresponds to solutions where the individuals are equally distributed only among two of the three shelters, the last one remaining empty. For S > N, two branches for x₁ are stable, corresponding to the solution where only one shelter harbors all of the individuals and the two others are, therefore, empty [(x₁ ≈ N, x₂ ≈ x₃ ≈ 0); (x₁ ≈ x₃ ≈ 0, x₂ ≈ N); (x₁ ≈ x₂ ≈ 0, x₃ ≈ N)]. The branches corresponding to an equal distribution between two or three shelters are unstable. For p = 4: compared to the previous case, one more stable branch occurs, corresponding to equipartition among the four shelters. When S increases, the cascade of new stable states corresponds to equipartition among three or two shelters. When S > N, the only stable state corresponds to one of the shelters harboring all of the individuals. During the emergence of steady states, zones of coexisting stable states are observed.

Fig. 4.

Optimal benefit associated with individual distributions between shelters of equal quality. (A) Benefit for two shelters. The benefit function takes into account the advantage of forming large groups and the costs of crowding and finding the sites (n = 2 in Eq. 7). When σ < 1, the maximum is observed for an equal distribution of individuals between the two shelters, even when the shelters can contain more than N/2 individuals. As σ increases, the benefit surface spreads x₁ ≈ x₂ ≈ N/2. The benefit maxima are found for all individuals in one of the shelters, thus maximizing group size. (B) Cascade of increasing benefit for two, three, and four shelters. We show the individual distribution in the shelters maximizing the benefit (Eq. 7). For a given value of σ, the benefit maximum is given by the steady-state distribution among shelters in accordance with the model for collective decision (Eqs. 3 and 4). For intermediate value of σ (≈0.5, ≈1.25) the individuals use only some of available shelters. The dynamics induces the emergence of rational distributions of the individuals among the available shelters. These population fractions maximize group sizes, minimize the number of shelters used, and take into account crowding effects and the probability of encountering the shelter.