Effects of preculturing conditions on lag time and specific growth rate of Enterobacter sakazakii in reconstituted powdered infant formula

Abstract

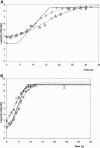
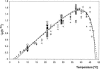
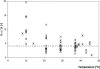
Enterobacter sakazakii can be present, although in low levels, in dry powdered infant formulae, and it has been linked to cases of meningitis in neonates, especially those born prematurely. In order to prevent illness, product contamination at manufacture and during preparation, as well as growth after reconstitution, must be minimized by appropriate control measures. In this publication, several determinants of the growth of E. sakazakii in reconstituted infant formula are reported. The following key growth parameters were determined: lag time, specific growth rate, and maximum population density. Cells were harvested at different phases of growth and spiked into powdered infant formula. After reconstitution in sterile water, E. sakazakii was able to grow at temperatures between 8 and 47 degrees C. The estimated optimal growth temperature was 39.4 degrees C, whereas the optimal specific growth rate was 2.31 h(-1). The effect of temperature on the specific growth rate was described with two secondary growth models. The resulting minimum and maximum temperatures estimated with the secondary Rosso equation were 3.6 degrees C and 47.6 degrees C, respectively. The estimated lag time varied from 83.3 +/- 18.7 h at 10 degrees C to 1.73 +/- 0.43 h at 37 degrees C and could be described with the hyperbolic model and reciprocal square root relation. Cells harvested at different phases of growth did not exhibit significant differences in either specific growth rate or lag time. Strains did not have different lag times, and lag times were short given that the cells had spent several (3 to 10) days in dry powdered infant formula. The growth rates and lag times at various temperatures obtained in this study may help in calculations of the period for which reconstituted infant formula can be stored at a specific temperature without detrimental impact on health.

FIG. 1.

(A) Predicted and measured growth curves of E. sakazakii ATCC 29544 at 21°C, precultured to mid-stationary phase. The different symbols indicate different replicate experiments. The solid line is the design growth curve at 21°C, calculated with the cardinal values shown in Table 1 under “initial estimate”; dotted lines represent fits of the modified Gompertz equation to each single experiment. (B) Predicted and measured growth curves of E. sakazakii ATCC 29544 at 37°C, precultured to mid-stationary phase. The different symbols indicate different replicate experiments. The solid line is the design growth curve at 37°C, calculated with the cardinal values shown in Table 1; dotted lines represent fits of the modified Gompertz equation to each single experiment.

FIG. 2.

(A) Square roots of specific growth rate data for various physiological growth phases of strain ATCC 29544 as a function of temperature. ×, lag-phase cells; ▵, exponential-phase cells; ⋄, early-stationary-phase cells; ×|, mid-stationary-phase cells; ○, stationary-phase cells; □, late-stationary-phase cells. (B) Log lag times for various physiological growth states of ATCC 29544 as a function of temperature. ×, lag-phase cells; ▵, exponential-phase cells; ⋄, early-stationary-phase cells; ×|, mid-stationary-phase cells; ○, stationary-phase cells; □, late-stationary-phase cells.

FIG. 3.

Square roots of measured and fitted specific growth rates as a function of temperature. Shown are growth rates of ATCC 29544 precultures to various growth phases, as estimated by the fit of the modified Gompertz model to each individual growth curve ○, and growth rates for mid-stationary-phase cells of MM9 •, S94 ♦, and MC10 ▴. Other symbols: +, growth rates published by Nazarowec-White and Farber (9); ⋄: growth rates published by Iversen et al. (5); dashed line, fit by the secondary growth model of Ratkowsky; dotted line, fit by the secondary growth model of Rosso (fitted to square root transformed data of the present study only).

FIG. 4.

Log lag times as a function of temperature. ○, ATCC 29544 precultures to various growth phases. Also shown are data for mid-stationary-phase cells of MM9 •, S94 ♦, and MC10 ▴; lag times at 10 and 23°C as published by Nazarowec-White and Farber (9) (+); and logarithmic transformed lag time data from the present study, modeled with the hyperbolic model (dashed line) and the reciprocal Ratkowsky model (solid line).

FIG. 5.

Parameter k (the product of λ and μ_m) as a function of temperature for each growth experiment with strain ATCC 29544 precultured to various growth phases and grown at temperatures from 8 to 47°C. ×, lag-phase cells; ▵, exponential-phase cells; ⋄, early-stationary-phase cells; ×|, mid-stationary-phase cells; ○, stationary-phase cells; □, late-stationary-phase cells. The dotted line represents the average value for the data from 20 to 46°C.

FIG. 6.

Initial inoculum of strain ATCC 29544 precultured to various physiological states and maximum population densities at various temperatures. ▵, maximum population density; ○, initial number of cells. The dotted line represents the average value for the maximum population density data from 8 to 46°C.