Mechanical properties of pore-spanning lipid bilayers probed by atomic force microscopy
- PMID: 16617084
- PMCID: PMC1479081
- DOI: 10.1529/biophysj.106.081398
Mechanical properties of pore-spanning lipid bilayers probed by atomic force microscopy
Abstract
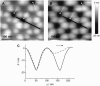
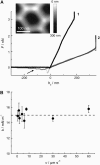
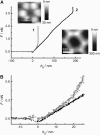
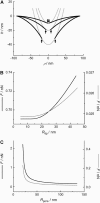
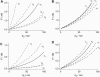
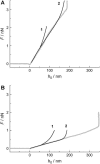
We measure the elastic response of a free-standing lipid membrane to a local indentation by using an atomic force microscope. Starting point is a planar gold-coated alumina substrate with a chemisorbed 3-mercaptopropionic acid monolayer displaying circular pores of very well defined and tunable size, over which bilayers composed of N,N,-dimethyl-N,N,-dioctadecylammonium bromide or 1,2-dioleoyl-3-trimethylammonium-propane chloride were spread. Centrally indenting these "nanodrums" with an atomic force microscope tip yields force-indentation curves, which we quantitatively analyze by solving the corresponding shape equations of continuum curvature elasticity. Since the measured response depends in a known way on the system geometry (pore size, tip radius) and on material parameters (bending modulus, lateral tension), this opens the possibility to monitor local elastic properties of lipid membranes in a well-controlled setting.
Figures




References
-
- Alessandrini, A., and P. Facci. 2005. AFM: a versatile tool in biophysics. Meas. Sci. Technol. 16:R65–R92.
-
- Butt, H.-J., B. Cappella, and M. Kappl. 2005. Force measurements with the atomic force microscope: Technique, interpretation and applications. Surf. Sci. Rep. 59:1–152.
-
- Janshoff, A., M. Neitzert, Y. Oberdörfer, and H. Fuchs. 2000. Force spectroscopy of molecular systems - single molecule spectroscopy of polymers and biomolecules. Angew. Chem. Int. Ed. Engl. 39:3346–3374. - PubMed
-
- Janshoff, A., and C. Steinem. 2001. Scanning force microscopy of artificial membranes. ChemBioChem. 2:798–808. - PubMed
-
- Boal, D. 2002. Mechanics of the Cell. Cambridge University Press, Cambridge.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

