Diffusion of isolated DNA molecules: dependence on length and topology

Abstract

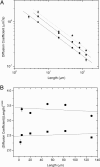
The conformation and dynamics of circular polymers is a subject of considerable theoretical and experimental interest. DNA is an important example because it occurs naturally in different topological states, including linear, relaxed circular, and supercoiled circular forms. A fundamental question is how the diffusion coefficients of isolated polymers scale with molecular length and how they vary for different topologies. Here, diffusion coefficients D for relaxed circular, supercoiled, and linear DNA molecules of length L ranging from approximately 6 to 290 kbp were measured by tracking the Brownian motion of single molecules. A topology-independent scaling law D approximately L(-nu) was observed with nu(L) = 0.571 +/- 0.014, nu(C) = 0.589 +/- 0.018, and nu(S) = 0.571 +/- 0.057 for linear, relaxed circular, and supercoiled DNA, respectively, in good agreement with the scaling exponent of nu congruent with 0.588 predicted by renormalization group theory for polymers with significant excluded volume interactions. Our findings thus provide evidence in support of several theories that predict an effective diameter of DNA much greater than the Debye screening length. In addition, the measured ratio D(Circular)/D(Linear) = 1.32 +/- 0.014 was closer to the value of 1.45 predicted by using renormalization group theory than the value of 1.18 predicted by classical Kirkwood hydrodynamic theory and agreed well with a value of 1.31 predicted when incorporating a recently proposed expression for the radius of gyration of circular polymers into the Zimm model.

Fig. 1.

Scaling of diffusion coefficients. (A) Diffusion coefficient (D) vs. chain length (L) for isolated DNA molecules. The points are the data obtained by tracking fluorescently labeled linear (squares), relaxed circular (circles), and untreated (mostly supercoiled circular) (triangles) DNA. The solid lines are power-law fits having exponents ν_L = 0.571 ± 0.014 and ν_C = 0.589 ± 0.018. The dashed line is a fit to the supercoiled DNA data with ν_S = 0.571 ± 0.057. The error bars indicate σ_D from bootstrap analysis. (B) Comparison of measured scaling of diffusion coefficient (D) with chain length (L) to predicted scaling of −0.588. Plot of D·L^0.588 vs. L (data points and error bars are the same as those in A). The solid lines are linear fits to the data that yield values of 6.27 × 10⁻⁴± 0.001 and −9.07 × 10⁻⁴± 0.001 for linear and circular molecules, respectively.

Fig. 2.

Agarose gel electrophoresis of YOYO-I-labeled pPIC9K〈TRL5〉 DNA samples containing an initial mixture of supercoiled (S) and relaxed circular (RC) species (A), a relaxed circular form produced by treatment with topoisomerase I (B), and a nicked circular form (C). The staining level was varied as follows (in base pairs per dye molecule): lane a, unlabeled DNA; lane b, 500:1; lane c, 50:1; lane d, 5:1; lane e, 1:2; lane f, 1:20; lane g, 1:200; lane h, 1:2,000. The samples were incubated in the dark for 2 h at 50°C to ensure homogeneous labeling. A 1% agarose gel was run using tris-acetate-EDTA buffer and poststained with ethidium bromide to make the bands uniformly visible.