A simple rule for the evolution of cooperation on graphs and social networks
- PMID: 16724065
- PMCID: PMC2430087
- DOI: 10.1038/nature04605
A simple rule for the evolution of cooperation on graphs and social networks
Abstract
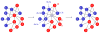
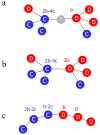
A fundamental aspect of all biological systems is cooperation. Cooperative interactions are required for many levels of biological organization ranging from single cells to groups of animals. Human society is based to a large extent on mechanisms that promote cooperation. It is well known that in unstructured populations, natural selection favours defectors over cooperators. There is much current interest, however, in studying evolutionary games in structured populations and on graphs. These efforts recognize the fact that who-meets-whom is not random, but determined by spatial relationships or social networks. Here we describe a surprisingly simple rule that is a good approximation for all graphs that we have analysed, including cycles, spatial lattices, random regular graphs, random graphs and scale-free networks: natural selection favours cooperation, if the benefit of the altruistic act, b, divided by the cost, c, exceeds the average number of neighbours, k, which means b/c > k. In this case, cooperation can evolve as a consequence of 'social viscosity' even in the absence of reputation effects or strategic complexity.
Figures

References
-
- Hamilton WD. The genetical evolution of social behaviour. J theor Biol. 1964;7:1–16. - PubMed
-
- Trivers R. The evolution of reciprocal altruism. Q Rev Biol. 1971;46:35–57.
-
- Axelrod R, Hamilton WD. The evolution of cooperation. Science. 1981;211:1390–1396. - PubMed
-
- Wilson EO. Sociobiology. Harvard Univ. Press; Cambridge, MA: 1975.
-
- Wedekind C, Milinski M. Cooperation through image scoring in humans. Science. 2000;288:850–852. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

