Dynamic deformation and recovery response of red blood cells to a cyclically reversing shear flow: Effects of frequency of cyclically reversing shear flow and shear stress level

Abstract

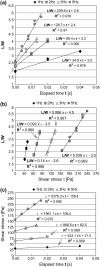
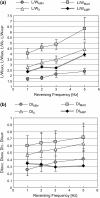
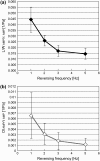
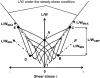
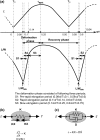
Dynamic deformation and recovery responses of red blood cells (RBCs) to a cyclically reversing shear flow generated in a 30-microm clearance, with the peak shear stress of 53, 108, 161, and 274 Pa at the frequency of 1, 2, 3, and 5 Hz, respectively, were studied. The RBCs' time-varying velocity varied after the glass plate velocity without any time lag, whereas the L/W change, where L and W were the major and minor axes of RBCs' ellipsoidal shape, exhibited a rapid increase and gradual decay during the deformation and recovery phase. The time of minimum L/W occurrence lagged behind the zero-velocity time of the glass plate (zero stress), and the delay time normalized to the one-cycle duration remained constant at 8.0%. The elongation of RBCs at zero stress time became larger with the reversing frequency. A simple mechanical model consisting of an elastic linear element during a rapid elongation period and a parallel combination of elements such as a spring and dashpot during the nonlinear recovery phase was suggested. The dynamic response behavior of RBCs under a cyclically reversing shear flow was different from the conventional shape change where a steplike force was applied to and completely released from the RBCs.

FIGURE 1

Schematic diagram of a CRSFG comprised of a slider-crank mechanism, a microscope data acquisition system, and a synchronized data acquisition system of RBC images with respect to a glass plate movement signal.

FIGURE 2

Assembled CRFGS showing the microscope stage mounted with a parallel glass plate assembly and a motor-cam system.

FIGURE 3

Typical RBC images under reversing shear flows. (i) Minimal elongation images, (ii) images remaining elongated when V_plate is zero (τ₀), and (iii) maximal elongation images under the reversing frequency of (a) 1 Hz, (b) 2 Hz, (c) 3 Hz, and (d) 5 Hz.

FIGURE 4

Time-course changes in the glass plate displacement, glass plate velocity V_plate, and RBC velocity V_RBC, generated shear stress, and RBC deformation L/W for reversing frequency of (a) 1 Hz, (b) 2 Hz, (c) 3 Hz, and (d) 5 Hz. For each frequency is shown (i) glass plate displacement and plate velocity V_plate, (ii) V_plate and V_RBC, and (iii) shear stress and L/W. The positive V_plate value indicates the glass plate motion toward the right in Fig. 2. In the figure, time 0 corresponds to when the slider block was closest to the gap sensor.

FIGURE 4

Time-course changes in the glass plate displacement, glass plate velocity V_plate, and RBC velocity V_RBC, generated shear stress, and RBC deformation L/W for reversing frequency of (a) 1 Hz, (b) 2 Hz, (c) 3 Hz, and (d) 5 Hz. For each frequency is shown (i) glass plate displacement and plate velocity V_plate, (ii) V_plate and V_RBC, and (iii) shear stress and L/W. The positive V_plate value indicates the glass plate motion toward the right in Fig. 2. In the figure, time 0 corresponds to when the slider block was closest to the gap sensor.

FIGURE 5

Linear regression analysis between V_plate and V_RBC. Hardly any time delay was observed between the two time-varying events.

FIGURE 6

RBC responses in L/W during the rapid and linear elongation periods of the deformation phase. (a) L/W versus time; (b) L/W versus shear stress; and (c) shear stress versus time. During the rapid L/W increase period, L/W increased linearly to both time and the shear stress. The rapid and linear elongation periods occurred twice during each cycle at 0.1–0.14 and 0.6–0.64 s for 1 Hz, 0.05–0.07 and 0.3–0.32 s for 2 Hz, 0.0396–0.0528 and 0.2046–0.2178 s for 3 Hz, and 0.02–0.032 and 0.12–0.132 s for 5 Hz.

FIGURE 7

L/W-change speed during the deformation phase and the recovery phase. L/W-change speed was derived from the change in the absolute value of L/W with respect to time (|d(L/W)|/dt) during the rapid elongation period of the deformation phase (0.1–0.14 and 0.6–0.64 normalized time), and during the recovery phase (0.46–0.58 normalized time) of Fig 4, a iii–d iii.

FIGURE 8

Two-dimensional display of shear stress versus L/W (τ-L/W) for reversing frequencies of 1, 2, 3, and 5Hz. The τ-L/W pattern rotated in the counterclockwise direction in the right-half plane, but in the clockwise direction in the left-half plane. Shown are the characteristic points for zero plate velocity (A), minimal L/W (B and D), and maximal shear stress (C and E).

FIGURE 9

RBC deformation expressed in L/W and DI versus reversing frequency. (a) L/W_MAX, L/W_MIN, L/W₀, and L/W_AMP versus reversing frequency and (b) DI_MAX, DI_MIN, DI₀, and DI_AMP versus reversing frequency.

FIGURE 10

Frequency response of RBCs to reversing shear flow. (a) L/W_AMP normalized to τ_AMP versus reversing frequency and (b) DI_AMP normalized to τ_AMP versus reversing frequency.

FIGURE 11

Shear stress-L/W plane display of RBC responses to reversing shear flows in comparison to the speculated response to the uniform shear flow.

FIGURE 12

Analysis of RBC responses to reversing shear flows. (a) Time course asymmetric L/W changes showing deformation and recovery phases. The deformation phase consisted of three periods: S1, the pre-rapid-elongation period (0.08 ≤ t/T ≤ 0.1, 0.58 ≤ t/T ≤ 0.6); S2, rapid and linear elongation periods: (0.1 ≤ t/T ≤ 0.14, 0.6 ≤ t/T ≤ 0.64); and S3, slow and nonlinear elongation period (0.14 ≤ t/T ≤ 0.25, 0.64 ≤ t/T ≤ 0.75). (b) Elastic element model representing the rapid and linear elongation period. (c) Viscoelastic element model representing the recovery phase.

FIGURE 13

Analysis of the predictions based on the constant elastic modulus model versus experimental data during the deformation phase for (a) 1 Hz, (b) 2 Hz, (c) 3 Hz, and (d) 5 Hz.