Mode shifts in the voltage gating of the mouse and human HCN2 and HCN4 channels
- PMID: 16777944
- PMCID: PMC1819464
- DOI: 10.1113/jphysiol.2006.110437
Mode shifts in the voltage gating of the mouse and human HCN2 and HCN4 channels
Abstract
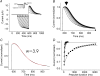
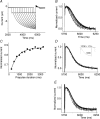
Hyperpolarization-activated, cyclic-nucleotide-gated (HCN) channels regulate pacemaker activity in the heart and the brain. Previously, we showed that spHCN and HCN1 channels undergo mode shifts in their voltage dependences, shifting the conductance versus voltage curves by more than +50 mV when measured from a hyperpolarized potential compared to a depolarized potential. In addition, the kinetics of the ionic currents changed in parallel to these voltage shifts. In the studies reported here, we tested whether slower cardiac HCN channels also display similar mode shifts. We found that HCN2 and HCN4 channels expressed in oocytes from the frog Xenopus laevis do not display the activation kinetic changes that we observed in spHCN and HCN1. However, HCN2 and HCN4 channels display changes in their tail currents, suggesting that these channels also undergo mode shifts and that the conformational changes underlying the mode shifts are due to conserved aspects of HCN channels. With computer modelling, we show that in channels with relatively slow opening kinetics and fast mode-shift transitions, such as HCN2 and HCN4 channels, the mode shift effects are not readily observable, except in the tail kinetics. Computer simulations of sino-atrial node action potentials suggest that the HCN2 channel, together with the HCN1 channel, are important regulators of the heart firing frequency and that the mode shift is an important property to prevent arrhythmic firing. We conclude that although all HCN channels appear to undergo mode shifts - and thus may serve to prevent arrhythmic firing - it is mainly observable in ionic currents from HCN channels with faster kinetics.
Figures

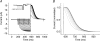


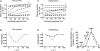

References
-
- Azene EM, Xue T, Marban E, Tomaselli GF, Li RA. Non-equilibrium behavior of HCN channels: insights into the role of HCN channels in native and engineered pacemakers. Cardiovasc Res. 2005;67:263–273. - PubMed
-
- Baruscotti M, Bucchi A, Difrancesco D. Physiology and pharmacology of the cardiac pacemaker (‘funny’) current. Pharmacol Ther. 2005;107:59–79. - PubMed
-
- Chen J, Mitcheson JS, Lin M, Sanguinetti MC. Functional roles of charged residues in the putative voltage sensor of the HCN2 pacemaker channel. J Biol Chem. 2000;275:36465–36471. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

